
19. (本小题满分13分) 
(Ⅰ) 设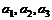 均为正数,且
均为正数,且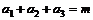 ,求证
,求证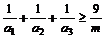 .
.
(Ⅱ) 求函数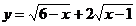 的最大值
的最大值
18. (本小题满分13分)
(Ⅰ) 已知不等式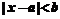 的解集是
的解集是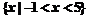

解不等式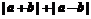 ≥
≥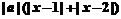



(Ⅱ)设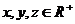 ,且x+2y+3z=36,求
,且x+2y+3z=36,求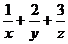 的最小值.
的最小值.
17.(本小题满分13分)
已知命题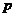 :方程
:方程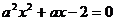 在[-1,1]上有解;命题
在[-1,1]上有解;命题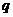 :只有一个实数
:只有一个实数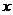 满足不等式
满足不等式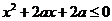 ,若命题“p或q”是假命题,求实数a的取值范围.
,若命题“p或q”是假命题,求实数a的取值范围.

16. (本小题满分13分)


记函数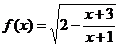 的定义域为
的定义域为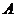 ,
, 的
的
定义域为B.
(Ⅰ)求集合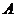 ;
;
(Ⅱ)若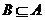 , 求实数
, 求实数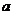 的取值范围.
的取值范围.

15.设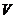 是已知平面
是已知平面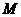 上所有向量的集合,对于映射
上所有向量的集合,对于映射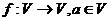 ,记
,记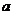 的象为
的象为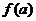 。若映射
。若映射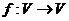 满足:对所有
满足:对所有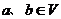 及任意实数
及任意实数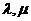 都有
都有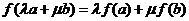 ,则
,则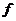 称为平面
称为平面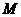 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设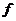 是平面
是平面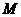 上的线性变换,
上的线性变换,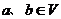 ,则
,则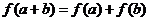

②若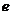 是平面
是平面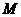 上的单位向量,对
上的单位向量,对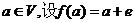 ,则
,则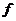 是平面
是平面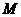 上的线性变换;
上的线性变换; 
③对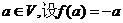 ,则
,则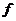 是平面
是平面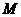 上的线性变换;
上的线性变换; 
④设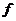 是平面
是平面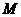 上的线性变换,
上的线性变换,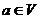 ,则对任意实数
,则对任意实数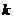 均有
均有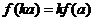 。
。
其中的真命题是
(写出所有真命题的编号)
14.已知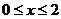 ,则函数
,则函数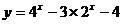 的最大值
的最大值 
13. 已知函数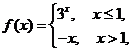 若
若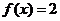 ,则
,则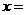 .
.
12.设集合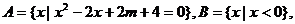 ,
,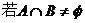 ,则实数m的取值范围__________;
,则实数m的取值范围__________;
11.已知集合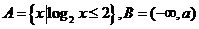 ,若
,若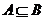 则实数
则实数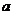 的取值范围是
的取值范围是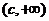 ,其中
,其中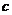 = .
= .

10.定义在R上的函数f(x)满足f(x)= 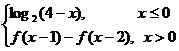 ,则f(3)的值为(
)
,则f(3)的值为(
)
A.-1
B. -2
C.1
D. 2 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com