21、购买某种保险，每个投保人每年度向保险公司交纳保费a 　 　元，若投保人在购买保险的一年度内出险，则可以获得10000元的赔偿金．假定在一年度内有10000人购买了这种保险，且各投保人是否出险相互独立．已知保险公司在一年度内至少支付赔偿金10000元的概率为1－0.999.(Ⅰ)求一投保人在一年度内出险的概率p；(Ⅱ)设保险公司开办该项险种业务除赔偿金外的成本为50000元，为保证盈利的期望不小于0，求每位投保人应交纳的最低保费(单位：元)．

20、二阶矩阵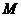对应变换将点(1，2)和(2，1)分别变换成(5，1)和(4，-1)。

(1)求矩阵；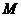

(2)求矩阵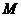将圆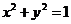变换后的方程。　 　

19、潮州统计局就某地居民的月收入调查了人，并根据所得数据画了样本的频率分

布直方图(每个分组包括左端点，不包括右端点，如第一组表示收入在)。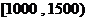

(1)求居民月收入在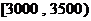的频率；　 　

(2)根据频率分布直方图算出样本数据的中位数；

(3)为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这人中用

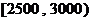分层抽样方法抽出人作进一步分析，则月收入在的这段应抽多少人？

18、甲、乙、丙三人参加了一家公司招聘面试，甲表示只要面试合格就签约；乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约，设每人面试合格的概率都是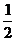，且面试是否合格互不影响。(1)求至少有一人面试合格的概率；(2)求签约人数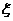的分布列和数学期望；

17、极坐标与参数方程：已知直线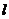的参数方程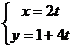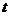：(为参数)，圆C的极坐标方程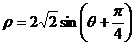：，试判断直线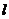与圆C的位置关系．　 　

16、已知：，().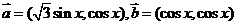

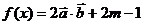(Ⅰ) 求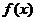关于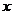的表达式，并求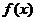的最小正周期；　 　

(Ⅱ) 若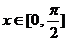时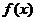，的最小值为5，求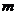的值.