
5. 一列横波沿x轴传播,t1与t2时刻的波形分别如图13-4中的实线和虚线所示,已知t2-t1=0.1s,那么这列波的速度可能是( )
一列横波沿x轴传播,t1与t2时刻的波形分别如图13-4中的实线和虚线所示,已知t2-t1=0.1s,那么这列波的速度可能是( )
|
4. 一质点从t=0时刻开始以坐标原点O为中心在y轴上做简谐运动,其振动图象如图1所示,0.3s后,此质点停止运动。振动在介质中产生的简谐横波沿x轴正方向传播,波速为1.0m/s,此质点停止振动后,再经过0.2s后的波形图是()
|
1.一列简谐横波向右传播,波速为v。沿波传播方向上有相距为L的P、Q两质点,如图所示。某时刻P、Q两质点都处于平衡位置,且P、Q间仅有一个波峰,经过时间t,Q质点第一次运动到波谷。则t的可能值( )
A.1个 B.2个 C.3个 D.4个
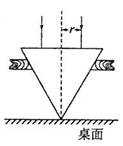
|
A.r B.1.5r
C.2r D.2.5r
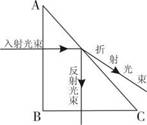
|
A.V1<V2 单色光束为红色 B.V1<V2 单色光束为蓝色
C.V1>V2 单色光束为红色 D.V1>V2 单色光束为蓝色
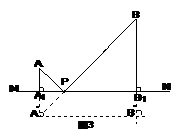 例4. 如图3所示,MN表示一条铁路,A,B是两个城市,它们到铁路所在直线,它们到铁路所在直线MN的垂直距离分别为
例4. 如图3所示,MN表示一条铁路,A,B是两个城市,它们到铁路所在直线,它们到铁路所在直线MN的垂直距离分别为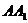 =20km,
=20km,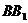 =40km,且
=40km,且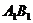 =80km.现要在
=80km.现要在 之间设一个中转站P,使两个城市到中转站的距离之和最短.请你设计一个方案确定P点的位置,并求出这个最短距离.
之间设一个中转站P,使两个城市到中转站的距离之和最短.请你设计一个方案确定P点的位置,并求出这个最短距离.
分析:本题为最佳方案设计题,要寻找点P的思路根据“两点之间线段最段”,只要将点A移到MN的另一侧即可,也就是A与点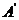 关于MN对称,此时PA=P
关于MN对称,此时PA=P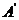 ,因此PA+PB= P
,因此PA+PB= P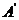 +PB=
+PB=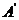 B,故点P到点A,B距离之和最短.
B,故点P到点A,B距离之和最短.
解:如图3,作点A关于MN的对称点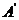 ,连接
,连接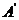 B,交MN于点P,则点P就是要确定的中转站的位置,最短距离即为PA+PB.
B,交MN于点P,则点P就是要确定的中转站的位置,最短距离即为PA+PB.
过点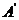 作
作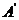
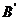 ⊥
⊥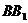 ,交
,交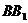 的延长线于
的延长线于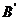 点.在Rt△
点.在Rt△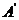 B
B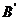 中,
中,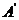
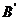 =
=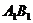 =80km,
=80km, =
=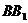 +
+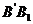 =
=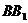 +
+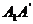 =
=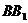 +
+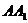 =40+20=60(km),所以
=40+20=60(km),所以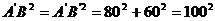 ,所以
,所以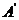 B=100km,由点的对称性可知AP+BP= P
B=100km,由点的对称性可知AP+BP= P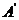 +PB=
+PB=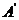 B=100km,所以这个最短距离为100km.
B=100km,所以这个最短距离为100km.
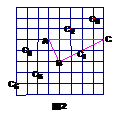 例3.如图2所示,是由边长为1的小正方形组成的正方形网格,以线段AB(A,B为格点)为一条直角边任
例3.如图2所示,是由边长为1的小正方形组成的正方形网格,以线段AB(A,B为格点)为一条直角边任 意画一个Rt△ABC,且点C为格点,并求出以BC为边的正方形的面积.
意画一个Rt△ABC,且点C为格点,并求出以BC为边的正方形的面积.
分析:这是一道结论开放题,据题意经过分析,符合要求的点C有多个,如图2所示, ,
,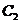 ,
,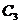 ,
,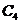 ,
,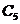 ,
,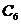 都是符合要求的点.
都是符合要求的点.
解:画出的Rt△ABC如图2中所示,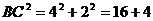 =20,所以以BC为边的正方形面积为20.
=20,所以以BC为边的正方形面积为20.
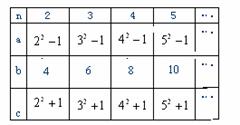 例2.张老师在一次“探究性学习”课中,设计了如下表:
例2.张老师在一次“探究性学习”课中,设计了如下表:
(1)请你分别观察a、b、c与n(n>1)
之间的关系,并分别用含n的代数式表示a、b、c:a= ,b= ,c= ;
(2)猜想以a、b、c为边的三角形是否
为直角三角形,并验证你的猜想.
解:(1)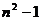 ;2n;
;2n;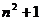
(2)猜想以a、b、c为边的三角形是直角三角形. 验证:由于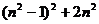
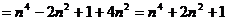 ,因为
,因为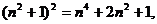 所以
所以
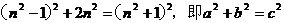 .故以a、b、c为边的三角形是直角三角形.
.故以a、b、c为边的三角形是直角三角形.
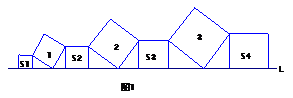 例1. 在直线L上依次摆放着七个正方形(如图1所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S
例1. 在直线L上依次摆放着七个正方形(如图1所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S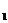 、S
、S 、S
、S 、S
、S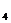 ,则S
,则S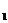 +S
+S +S
+S +S
+S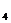 =
.
=
.
分析: 经过观察图形,可以看出正放着正方形面积与斜放置的正方形之间关系为: S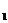 +S
+S =1; S
=1; S +S
+S =2; S
=2; S +S
+S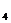 =3;这样数形结合可把问题解决.
=3;这样数形结合可把问题解决.
解: S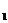 代表的面积为S
代表的面积为S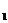 的正方形边长的平方, S
的正方形边长的平方, S 代表的面积为S
代表的面积为S 的正方形边长的平方,所以S
的正方形边长的平方,所以S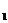 +S
+S =斜放置的正方形面积为1;同理S
=斜放置的正方形面积为1;同理S +S
+S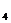 =斜放置的正方形面积为3,故S
=斜放置的正方形面积为3,故S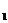 +S
+S +S
+S +S
+S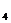 =1+3=4.
=1+3=4.
22.(本小题满分14分)集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若B⊆A,求实数m的取值范围;
(2)当x∈Z,求A的非空真子集个数;
(3)当x∈R时,没有元素x使x∈A与x∈B同时成立,求实数m的取值范围.
解:(1)当m+1>2m-1,即m<2时,B=∅满足B⊆A;
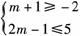 当m+1≤2m-1,即m≥2时,要使B⊆A成立,
当m+1≤2m-1,即m≥2时,要使B⊆A成立,
需 ,可得2≤m≤3.
综上,当m≤3时有B⊆A.
(2)当x∈Z时,A={-2,-1,0,1,2,3,4,5}.
∴A的非空真子集个数为28-2=254.
(3)∵x∈R,且没有元素x使x∈A与x∈B同时成立.
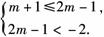
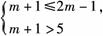 则①若B=∅,即m+1>2m-1,得m<2时满足条件.
则①若B=∅,即m+1>2m-1,得m<2时满足条件.
②若B≠∅,则要满足条件 或 解之,得m>4.
综上,有m<2或m>4.
21.(本小题满分12分)已知函数f(x)= 的定义域为集合A,函数g(x)=lg(-x2 +2x+m)的定义域为集合B.
(1)当m=3时,求A∩(∁RB);
(2)若A∩B={x|-1<x<4},求实数m的值.
解:A={x|-1<x≤5}.
(1)当m=3时,B={x|-1<x<3},
则∁RB={x|x≤-1或x≥3},
∴A∩(∁RB)={x|3≤x≤5}.
(2)∵A={x|-1<x≤5},
A∩B={x|-1<x<4},
∴有-42+2×4+m=0,解得m=8,
此时B={x|-2<x<4},符合题意.
20.(本小题满分12分)设命题p:函数f(x)=lg(ax2-x+a)的定义域为R;命题q:不等式<1+ax对一切正实数均成立,如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围.
解:命题p为真命题⇔函数f(x)=lg(ax2-x+a)的定义域为R,
即ax2-x+a>0对任意实数x均成立,
 得a=0时,-x>0的解集为R,不可能;
得a=0时,-x>0的解集为R,不可能;
或者 ⇔a>2.
所以命题p为真命题⇔a>2.
命题q为真命题⇔-1<ax对一切正实数均成立,
即a>=对一切正实数x均成立,
由于x>0,所以>1.
所以+1>2,所以<1.
所以,命题q为真命题⇔a≥1.
∵p或q为真命题,p且q为假命题,
∴p、q一真一假.
若p为真命题,q为假命题,无解;
若p为假命题,q为真命题,则1≤a≤2.
∴a的取值范围是[1,2].
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com