1.数列、、2、…，则2是该数列的　　　　　　　　　　　　　　　 (　)

A．第6项　 　　　B．第7项　　　 C．第10项　 　D．第11项

解析：原数列可写成、、，….

∵2＝，∴20＝2+(n－1)×3，∴n＝7.

答案：B

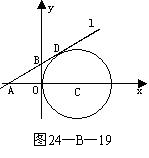
24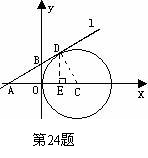．解：如图所示，连接CD，∵直线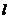为⊙C的切线，∴CD⊥AD。

∵C点坐标为(1，0)，∴OC=1，即⊙C的半径为1，∴CD=OC=1。

又∵点A的坐标为(-1，0)，∴AC=2，∴∠CAD=30°。

作DE⊥AC于E点，则∠CDE=∠CAD=30°，

∴CE=，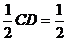

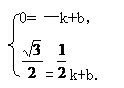
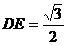，∴OE=OC-CE=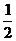，∴点D的坐标为(，)。

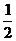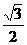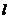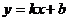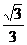设直线的函数解析式为，则　　　　　　　　 解得k=，b=，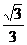

∴直线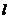的函数解析式为y=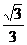x+.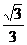

23．(1)证明：连接OD，∵AB是直径，AB⊥CD，∴∠COB=∠DOB=。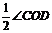

又∵∠CPD=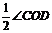，∴∠CPD=∠COB。

(2)∠CP′D与∠COB的数量关系是：∠CP′D+∠COB=180°。

证明：∵∠CPD+∠CP′D=180°，∠CPD=∠COB，∴∠CP′D+∠COB=180°。

22．证法一：分别连接OA、OB。

∵OB=OA，∴∠A=∠B。又∵AC=BD，∴△AOC≌△BOD，∴OC=OD，

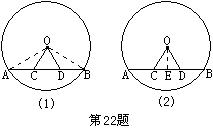
证法二：过点O作OE⊥AB于E，∴AE=BE。∵AC=BD，∴CE=ED，∴△OCE≌△ODE，∴OC=OD。

21．如图所示

11．50°　　 12．3　　 13．相等　　 14．100°　　 15．45°　　 16．4　　 17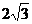． 18．AB//OC 　19．4　　 20．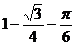

1．A　　 2．C　　 3．D　　 4．D　　 5．A　　 6．B　　 7．B　　 8．C　　 9．B　 10．C

24．如图24-A-19，在平面直角坐标系中，⊙C与y轴相切，且C点坐标为(1，0)，直线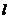过点A(-1，0)，与⊙C相切于点D，求直线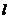的解析式。

第二十四章圆(B)

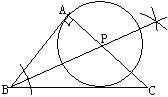
23．如图24-B-18，在⊙O中，AB是直径，CD是弦，AB⊥CD。

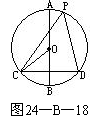(1)P是优弧CAD上一点(不与C、D重合)，求证：∠CPD=∠COB；

(2)点P′在劣弧CD上(不与C、D重合)时，∠CP′D与∠COB有什么数量关系？请证明你的结论。

22．如图24-B-17，AB是⊙O的弦(非直径)，C、D是AB上的两点，并且AC=BD。求证：OC=OD。