11．(文)数列{a_n}满足a_n+a_n+1＝(n∈N^*)，a₂＝2，S_n是数列{a_n}的前n项和，则S₂₁＝________.

解析：a₁＝－a₂＝－2，a₂＝2，a₃＝－2，a₄＝2，…，

知数列为周期数列，周期T＝2，a₁+a₂＝，

∴S₂₁＝10×+a₁＝5+－2＝.

答案：

(理)已知函数f(n)＝且a_n＝f(n)+f(n+1)，则a₁+a₂+a₃+…+a₁₀₀＝________.

解析：当n为奇数时，a_n＝n²－(n+1)²＝－(2n+1)，当n为偶数时，a_n＝－n²+(n+1)²＝2n+1，

∴a_n＝(－1)ⁿ(2n+1)，

∴a₁+a₂+…+a₁₀₀＝－3+5－7+…－199+201＝2×50＝100.

答案：100

10．(2010·温州模拟)设数列{a_n}的前n项和为S_n，令T_n＝，称T_n为数列a₁，a₂，…，a_n的“理想数”，已知数列a₁，a₂，…，a₅₀₁的“理想数”为2008，那么数列2，a₁，a₂…，a₅₀₁的“理想数”为　　　　　　　　　　　　　　　　 (　)

A．2004 　　　　B．2006　　　　　 C．2008 　　　　　　D．2010

解析：∵a₁，a₂，…，a₅₀₁的“理想数”为2008，

∴＝2008，

∴2，a₁，a₂…，a₅₀₁的理想数为

＝

＝2+

＝2+4×501＝2006.

答案：B

9.已知数列{a_n}的通项公式是a_n＝，其中a、b均为正常数，那么a_n与a_n+1的大小关系是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．a_n＞a_n+1 　B．a_n＜a_n+1

C．a_n＝a_n+1　 　　　　　　　　　D．与n的取值有关

解析：＝÷＝＝＜1，∵a_n+1＞0，∴a_n＜a_n+1.

答案：B

8．根据下列各个数列{a_n}的首项和基本关系式，求其通项公式．

(1)a₁＝1，a_n＝a_n－1+3^n－1(n≥2)；

(2)a₁＝1，a_n＝a_n－1(n≥2)．

解：(1)∵a_n＝a_n－1+3^n－1，

∴a_n－1＝a_n－2+3^n－2，

a_n－2＝a_n－3+3^n－3，

…

a₂＝a₁+3¹.

以上(n－1)个式子相加得

a_n＝a₁+3¹+3²+…+3^n－1

＝1+3+3²+…+3^n－1＝.

(2)∵a_n＝a_n－1(n≥2)，

∴a_n－1＝a_n－2，

…

a₂＝a₁.

以上(n－1)个式子相乘得

a_n＝a₁··……＝＝.

7．在数列{a_n}中，a₁＝1，a₂＝5，a_n+2＝a_n+1－a_n(n∈N^*)，则a_{1 000}＝　　　　　 (　)

A．5　 　　　B．－5 　　　C．1 　　　D．－1

解析：由a₁＝1，a₂＝5，a_n+2＝a_n+1－a_n(n∈N^*)，可得该数列为1,5,4，－1，－5，－4,1,5,4，….此数列为周期数列，由此可得a_{1 000}＝－1.

答案：D

6.在数列{a_n}中，a₁＝2，a_n+1＝a_n+ln(1+)，则a_n＝　　　　　　　　　　　　　 (　)

A．2+lnn 　　B．2+(n－1)lnn　　 C．2+nlnn　 　　D．1+n+lnn

解析：法一：由已知，a_n+1－a_n＝ln，a₁＝2，

∴a_n－a_n－1＝ln，

a_n－1－a_n－2＝ln，

……

a₂－a₁＝ln，

将以上n－1个式子累加得：

a_n－a₁＝ln+ln+…+ln

＝ln(··…·)＝lnn，

∴a_n＝2+lnn.

法二：由a₂＝a₁+ln2＝2+ln2，排除C、D；

由a₃＝a₂+ln(1+)＝2+ln3，排除B.

答案：A

5．已知数列{a_n}的前n项和S_n＝－n²+24n(n∈N^?)．

(1)求{a_n}的通项公式；

(2)当n为何值时，S_n达到最大？最大值是多少？

解：(1)n＝1时，a₁＝S₁＝23；

n≥2时，a_n＝S_n－S_n－1＝－2n+25.

经验证，a₁＝23符合a_n＝－2n+25，

∴a_n＝－2n+25(n∈N^?)．

(2)法一：∵S_n＝－n²+24n＝－(n－12)²+144，

∴n＝12时，S_n最大且S_n＝144.

法二：∵a_n＝－2n+25，

∴a_n＝－2n+25＞0，有n＜，

∴a₁₂＞0，a₁₃＜0，故S₁₂最大，最大值为144.

4.(2010·福州模拟)已知数列{a_n}的前n项和S_n＝n²－9n，第k项满足5＜a_k＜8，则k＝(　)

A．9　 　　　B．8　 　　　　C．7 　　　　　D．6

解析：a_n＝

＝

∵n＝1时适合a_n＝2n－10，

∴a_n＝2n－10.

∵5＜a_k＜8，∴5＜2k－10＜8，

∴＜k＜9.

又∵k∈N^*，∴k＝8.

答案：B

3．n个连续自然数按规律排成下表：

　 0　 3　→　 4　 7　→　 8　11　…

　 ↓　 　↑　 　　↓　 　↑　 　　↓　 　↑

　 　1 → 　2 　　　5 →　 　6　 　　9 →　 　10

根据规律，从2 009到2 011的箭头方向依次为　　　　　　　　　　　　　 (　)

A．↓→　　　　　　B．→↑

C．↑→　　　　　　　　　　 　D．→↓

解析：观察4的倍数0,4,8，…的位置．由于2 009＝4×502+1，故2 009在箭头↓的下方，从而2 009与2 010之间是箭头→，2 010与2 011之间是箭头↑.

答案：B

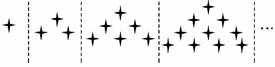
2．下列关于星星的图案构成一个数列，该数列的一个通项公式是　　　　　　　 (　)

A．a_n＝n²－n+1 　　　　　　　　　　　B．a_n＝

C．a_n＝　 　　　　　　　　　　　D．a_n＝

解析：从图中可观察星星的构成规律，

n＝1时，有1个；n＝2时，有3个；

n＝3时，有6个；n＝4时，有10个；…

∴a_n＝1+2+3+4+…+n＝.

答案：C