1．基础知识

蛋白质的物化理性质：形状、大小、电荷性质和多少、溶解度、吸附性质、亲和力等千差万别，由此提取和分离各种蛋白质。

蛋白质是生命活动的主要承担者，是细胞内含量最高的有机化合物。对蛋白质的研究有助于人们对生命过程的认识和理解。所以需要从细胞中提取蛋白质进行研究。怎样提取蛋白质呢？

13.读我国某能源和重化工基地图，回答下列问题。　

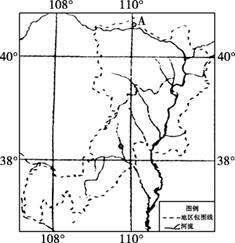
(1)说明图中A处成为钢铁工业基地的区位因素。　

(2)图示地区发展工业的优势区位因素有哪些？　

(3)图中虚线包围的地区，在能源重化工业基地的发展与建设中面临的重大问题有哪些？应如何解决？　　

　　 下图为鞍山市部分工业企业分布图，读图回答10~11题。　

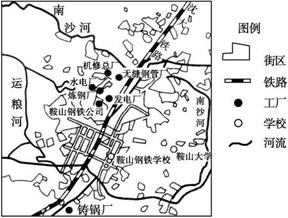
10.20世纪50年代鞍山已成为我国重要的钢铁基地,其形成的主要区位优势是　　　 (　　 )

A.高科技力量雄厚　　　　　　　　　 B.水陆交通便利　

C.水资源丰富　　　　　　　　　　　 D.矿产资源丰富

11.图中各企业高度集聚的最主要原因是　　　　　　　　　　　　　　　　　　　 (　　 )

A.存在生产工序上的联系

B.交通便利，便于集聚　

C.共用劳动力

D.集中治理工业污染

　　 读欧洲部分区域简图，回答8~9题。　

8.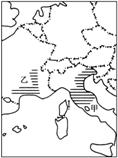甲为新兴工业区，与传统工业区相比，该区　　　　　　 (　　 )

A.资本集中程度高　

B.以大中型企业为主　

C.生产过程较分散　

D.以高技术工业为主　

9.与图中乙处经济作物密切相关的工业部门是　　　　　　 (　　 )

A.家具制造业　　　　　　　　　　　 B.葡萄酒酿造业　

C.服装工业　　　　　　　　　　　　 D.制糖工业

下图表示某地区工业发展不同阶段的生产与销售情况。读图，回答6~7题。　

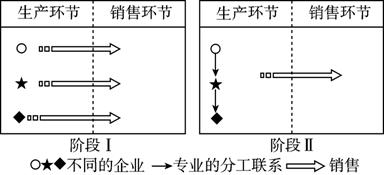
6.阶段Ⅰ，该地区企业生产特点有　　　　　　　　　　　　　　　　　　　　　　 (　　 )

①专业分工程度低　 ②总体生产能力强　 ③各企业团结协作　 ④各企业之间联系少　

A.①②　　　　　　　　　　　　　　　 B.②③　

C.③④　　　　　　　　　　　　　　　 D.①④　

7.阶段Ⅱ与阶段Ⅰ相比，该地区企业发展的优势有　　　　　　　　　　　　　　　 (　　 )

①环境污染减轻　 ②原料渠道拓宽　 ③规模效益增强　④交易成本降低　

A.①②　　　　　　　　　　　　　　 B.②③　

C.③④　　　　　　　　　　　　　 D.①④

　　 (2010年丹东模拟)下图是“某跨国公司工业投资地域变化图”，a、d两国均为发达国家，b、c两国均为发展中国家。读图，完成3~5题。　

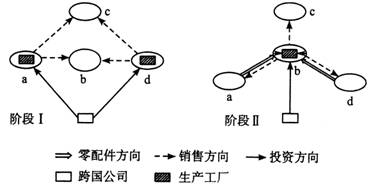
3.在阶段Ⅰ，影响跨国公司投资设厂的主导因素是　　　　　　　　　　　　　　　 (　　 )

A.市场　　 　　　　　　　　　　B.劳动力　

C.科技水平　　　　　　　　　　 D.原材料

4.在阶段Ⅱ，影响跨国公司投资设厂的主导因素是　　　　　　　　　　　　　　　 (　　 )

A.市场　　　　　　　　　　　　　 B.劳动力　

C.科技水平　　　　　　　　　　　 D.原材料

5.跨国公司投资地域变化，说明了　　　　　　　　　　　　　　　　　　　　　 (　　 )

A.发展中国家政局不稳，是投资变化的主要原因　

B.劳动力丰富是发展中国家发展经济唯一的区位优势　

C.跨国公司进行全球化经营使世界经济陷入混乱状态　

D.不同时期影响同一产业区位选择的因素也可能不同

　　 (2010年南通调研)图1为“美国‘硅谷’地区图”，图2为“鲁尔区图”，读图，完成1~2题。　

　 图1　　　　　　　　　　　　　 图2　

1.两地区工业共同的优势区位条件是　　　　　　　　　　　　　　　　　　　　 (　　 )

A.劳动力丰富　　　　　　　 B.交通便捷　

C.气候宜人　　　　　　　　 D.水源充足　

2.两工业地域形成与发展的共同特点是　　　　　　　　　　　　　　　　　　　 (　　 )

A.因生产联系而集聚　

B.经历了衰落、重振过程　

C.新增企业以中小型为主　

D.工业布局趋向原料产地

22．(文)(本小题满分14分)已知函数y＝f(x)的图象经过坐标原点，且f(x)＝x²－x+b，数列{a_n}的前n项和S_n＝f(n)(n∈N^*)．

(1)求数列{a_n}的通项公式；

(2)若数列{b_n}满足a_n+log₃n＝log₃b_n，求数列{b_n}的前n项和T_n；

(3)设P_n＝a₁+a₄+a₇+…+a_3n－2，Q_n＝a₁₀+a₁₂+a₁₄+…+a_2n+8，其中n∈N^*，试比较P_n与Q_n的大小，并证明你的结论．

解：(1)因为y＝f(x)的图象过原点，所以f(x)＝x²－x.

所以S_n＝n²－n，

当n≥2时，a_n＝S_n－S_n－1＝n²－n－(n－1)²+(n－1)＝2n－2，

又因为a₁＝S₁＝0适合a_n＝2n－2，

所以数列{a_n}的通项公式为a_n＝2n－2(n∈N^*)．

(2)由a_n+log₃n＝log₃b_n得：b_n＝n·3a_n＝n·3^2n－2(n∈N^*)，

所以T_n＝b₁+b₂+b₃+…+b_n＝3⁰+2·3²+3·3⁴+…+n·3^2n－2，9T_n＝3²+2·3⁴+3·3⁶+…+n·3²ⁿ.

两式相减得：8T_n＝n·3²ⁿ－(1+3²+3⁴+3⁶+…+3^2n－2)＝n·3²ⁿ－，

所以T_n＝－＝.

(3)a₁，a₄，a₇，…，a_3n－2组成以0为首项，6为公差的等差数列，所以P_n＝×6＝3n²－3n；

a₁₀，a₁₂，a₁₄，…，a_2n+8组成以18为首项，4为公差的等差数列，所以Q_n＝18n+×4＝2n²+16n.

故P_n－Q_n＝3n²－3n－2n²－16n＝n²－19n＝n(n－19)，

所以，对于正整数n，当n≥20时，P_n>Q_n；

当n＝19时，P_n＝Q_n；

当n<19时，P_n<Q_n.

(理)(本小题满分14分)已知数列{a_n}的前n项和为S_n，点(a_n+2，S_n+1)在直线y＝4x－5上，其中n∈N^*.令b_n＝a_n+1－2a_n，且a₁＝1.

(1)求数列{b_n}的通项公式；

(2)若f(x)＝b₁x+b₂x²+b₃x³+…+b_nxⁿ，求f′(1)的表达式，并比较f′(1)与8n²－4n的大小．

解：(1)∵S_n+1＝4(a_n+2)－5，∴S_n+1＝4a_n+3，

∴S_n＝4a_n－1+3(n≥2)，

∴a_n+1＝4a_n－4a_n－1(n≥2)，

∴a_n+1－2a_n＝2(a_n－2a_n－1)(n≥2)，

∴＝＝2(n≥2)．

∴数列{b_n}为等比数列，其公比为q＝2，首项b₁＝a₂－2a₁，

而a₁+a₂＝4a₁+3，且a₁＝1，∴a₂＝6，

∴b₁＝6－2＝4，

∴b_n＝4×2^n－1＝2ⁿ⁺¹.

(2)∵f(x)＝b₁x+b₂x²+b₃x³+…+b_nxⁿ，

∴f′(x)＝b₁+2b₂x+3b₃x²+…+nb_nx^n－1，

∴f′(1)＝b₁+2b₂+3b₃+…+nb_n，

∴f′(1)＝2²+2·2³+3·2⁴+…+n·2ⁿ⁺¹，　　　　　　　　　　　　　　　　　　 ①

∴2f′(1)＝2³+2·2⁴+3·2⁵+…+n·2ⁿ⁺²，　　　　　　　　　　　　　　　　　　 ②

①－②得

－f′(1)＝2²+2³+2⁴+…+2ⁿ⁺¹－n·2ⁿ⁺²

＝－n·2ⁿ⁺²＝－4(1－2ⁿ)－n·2ⁿ⁺²，

∴f′(1)＝4+(n－1)·2ⁿ⁺²，

∴f′(1)－(8n²－4n)＝4(n－1)·2ⁿ－4(2n²－n－1)

＝4(n－1)[2ⁿ－(2n+1)]．

当n＝1时，f′(1)＝8n²－4n；

当n＝2时，f′(1)－(8n²－4n)＝4(4－5)＝－4<0，f′(1)<8n²－4n；

当n＝3时，f′(1)－(8n²－4n)>0，

结合指数函数y＝2^x与一次函数y＝2x+1的图象知，当x>3时，总有2^x>2x+1，

故当n≥3时，总有f′(1)>8n²－4n.

综上：当n＝1时，f′(1)＝8n²－4n；

当n＝2时，f′(1)<8n²－4n；

当n≥3时，f′(1)>8n²－4n.