
5. 函数y=x4-4x+3在区间[-2,3]上的最小值为
A. 72 B. 36 C. 12 D.0
4. 已知集合P={x|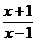 >0},集合Q={x|x2+x-2≥0},则x
>0},集合Q={x|x2+x-2≥0},则x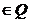 是x
是x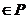 的
的
A、是充分条件但不是必要条件 B、是必要条件但是不充分条件
C、充要条件 D、既不是充分条件又不是必要条件
3. 函数f(x)=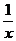 -x的图象关于
-x的图象关于
A 。 y轴对称 B.直线y=-x对称 C. 坐标原点对称 D. 直线y=x对称
2. 计算 的值为
的值为
A.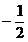 B.
B. C.
C.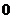 D.
D.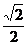
1.已知集合 ,则
,则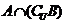 =
=
A.(2,3) (3,4) B.(2,4) C.(2,3)
(3,4) B.(2,4) C.(2,3) (3,4] D.(2,4]
(3,4] D.(2,4]
(五)作业1、复习本节课文
2、教材练习四第(1)、(2)、(3)题。
(四)课堂小结
(三)巩固练习
1.甲、乙两同学分别用竹竿击打湖面,湖面上就产生两列水波,那么,在两列水波相遇处,会获得稳定的干涉图样吗?为什么?
2.如图1所示,相干波源S1、S2发出的两列波,在介质中相遇叠加,实线表示这两列波的波峰中央,虚线表示这两列波的波谷中央。问图中A、B、C、P四个质点,哪些点振动最强?哪些点振动最弱?
我们有这样的生活经验:将两块石子投到水面上的两个不同地方,会激起两列圆形水波。它们相遇时会互相穿过,各自保持圆形波继续前进,与一列水波单独传播时的情形完全一样,这两列水波互不干扰。
[板书]二、波的干涉
一般地说,振动频率、振动方向都不相同的几列波在介质中叠加时,情形是很复杂的。我们只讨论一种最简单的但却是最重要的情形,就是两个振动方向、振动频率都相同的波源所发出的波的叠加。
[演示]在发波水槽实验装置中,振动着的金属薄片AB,使两个小球S1、S2同步地上下振动,由于小球S1、S2与槽中的水面保持接触,构成两个波源,水面就产生两列振动方向相同、频率也相同的波,这样的两列波相遇时产生的现象如课本图10-29所示。为什么会产生这种现象呢?我们可以用波的叠加原理来解释。
课本图10-30所示的是产生上述现象的示意图。S1和S2表示两列波的波源,它们所产生的波分别用两组同心圆表示,实线圆弧表示波峰中央,虚线圆弧表示波谷中央。某一时刻,如果介质中某点正处在这两列波的波峰中央相遇处[课本图10-30所示中的a点],则该点(a点)的位移是正向最大值,等于两列波的振幅之和。经过半个周期,两列波各前进了半个波长的距离,a点就处在这两列波的波谷中央相遇处,该点(a点)的位移就是负向最大值。再经过半个周期,a点又处在两列波的波峰中央相遇处。这样,a点的振幅就等于两列波的振幅之和,所以a点的振动总是最强的。这些振动最强的点都分布在课本图10-30中画出的粗实线上。某一时刻,介质中另一点如果正处在一列波的波峰中央和另一列波的波谷中央相遇处[课本图10-30中的b点],该点位移等于两列波的振幅之差。经过半个周期,该点就处在一列波的波谷中央和另一列波的波峰中央相遇处,再经过半个周期,该点又处在一列波的波峰中央和另一列波的波谷中央相遇处。这样,该点振动的振幅就等于两列波的振幅之差,所以该点的振动总是最弱的。如果两列波的振幅相等,这一点的振幅就等于零。这就是为什么在某些区域水面呈现平静的原因。这些振动最弱的点都分布在课本图10-30中画出的粗虚线上。可以看出,振动最强的区域和振动最弱的区域是相互间隔开的。
频率相同的波,叠加时形成某些区域的振动始终加强,另一些区域的振动始终减弱,并且振动加强和振动减弱的区域相互间隔,这种现象叫做波的干涉(inerference)。形成的图样叫做干涉图样。
只有两个频率相同、振动方向相同的波源发出的波,叠加时才会获得稳定的干涉图样,这样的波源叫做相干波源,它们发出的波叫做相干波。
不仅水波,一切波都能发生干涉,干涉现象是一切波都具有的重要特征之一。
[演示]敲击音叉使其发声,然后转动音叉,就可以听到声音忽强忽弱。这就是声波的干涉现象。
[板书]1、频率相同的波,叠加时形成某些区域的振动始终加强,另一些区域的振动始终减弱,并且振动加强和振动减弱的区域相互间隔,这种现象叫做波的干涉。形成的图样叫做干涉图样。
2、干涉现象是一切波都具有的现象。
3、 产生干涉的必要条件:两列波的频率必须相同。
产生干涉的必要条件:两列波的频率必须相同。
(二)进行新课
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com