
21.已知函数
(1)若函数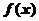 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;
(2)讨论函数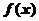 的单调性;
的单调性;
(3)当 时,求证:对大于
时,求证:对大于 的任意正整数
的任意正整数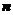 ,都有
,都有 。
。
选答题(本小题满分10分)(请考生在第22、23、24三道题中任选一题做答,并用2B铅笔在答题卡上把所选题目的题号涂黑。注意所做题号必须与所涂题目的题号一致,并在答题卡指 定区域答题。如果多做,则按所做的第一题计分。)
定区域答题。如果多做,则按所做的第一题计分。)
20.(本小题满分12分)
在平面直角坐标系中,已知 ,若实数
,若实数 使得
使得 (
( 为坐标原点)
为坐标原点)
(1)求 点的轨迹方程,并讨论
点的轨迹方程,并讨论 点的轨迹类型;
点的轨迹类型;
(2)当 时,若过点
时,若过点 的直线
的直线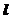 与(1)中
与(1)中 点的轨迹交于不同的两点
点的轨迹交于不同的两点 (
( 在
在 之间),试求
之间),试求 与
与 面积之比的取值范围。
面积之比的取值范围。
19.(本小题满分12分)
 如图,在直三棱柱
如图,在直三棱柱 中,
中, ,
, 为
为 的中点,且
的中点,且 ,
,
(1)当 时,求证:
时,求证: ;
;
(2)当 为何值时,直线
为何值时,直线 与平面
与平面 所成的角
所成的角
的正弦值为 ,并求此时二面角
,并求此时二面角 的余弦值。
的余弦值。
18.(本小题满分12分)
 某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有
某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有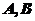 两个等级.对每种产品,两道工序的加工结果都为
两个等级.对每种产品,两道工序的加工结果都为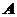 级时,产品为一等品,
级时,产品为一等品,
其余均为二等品。
(1)已知甲、乙两种产品每一道工序的加工结果为
A级的概率如表一所示,分别求生产出的甲、
乙产品为一等品的概率 ;
;
 (2)已知一件产品的利润如表二所示,用
(2)已知一件产品的利润如表二所示,用 分别
分别
表示一件甲、乙产品的利润,在(1)的条件
下,求 的分布列及
的分布列及 ;
;
(3)已知生产一件产品需用的工人数和资金额如
表三
|
 名,可用资金
名,可用资金
 万元。
万元。
|
 设
设 分别表示生产甲、乙产品的
分别表示生产甲、乙产品的
数量,在(2)的条件下, 为何值时,
为何值时,
 最大?最大值是多少?
最大?最大值是多少?
(解答时须给出图示说明)
17.(本小题满分12分)
已知函数 。
。
(1)若方程 在
在 上有解,求
上有解,求 的取值范围;
的取值范围;
(2)在 中,
中, 分别是
分别是 所对的边,当(1)中的
所对的边,当(1)中的 取最大值,且
取最大值,且 时,求
时,求 的最小值。
的最小值。
16.给出下列五个命题:
①设 ,则
,则 且
且 的充要条件是
的充要条件是 且
且 ;
;
②已知 ,若
,若 ,则满足
,则满足 的概率为
的概率为 ;
;
③命题“ ”的否定是“
”的否定是“ ”;
”;
 ④若随机变量
④若随机变量 -
- 且
且 ,则
,则 ;
;
⑤已知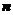 个散点
个散点 的线性回归方程为
的线性回归方程为 ,若
,若 ,(其中
,(其中 ,
, ),则此回归直线必经过点(
),则此回归直线必经过点( )。
)。
其中正确命题是 。
15.学校计划在五天里安排三节不同的选修课,且在同一天安排的选修课不超过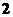 节,则不同的选修课安排方案有
种。
节,则不同的选修课安排方案有
种。
14.已知 ,则
,则 展开式中的常数项为___________。
展开式中的常数项为___________。
13.已知幂函数 的图象与
的图象与 轴、
轴、 轴无交点且关于原点对称,则
轴无交点且关于原点对称,则 ___________。
___________。
12.已知直线 与双曲线
与双曲线 ,有如下信息:联立方程组
,有如下信息:联立方程组 消去
消去 后得到方程
后得到方程 ,分类讨论:(1)当
,分类讨论:(1)当 时,该方程恒有一解;(2)当
时,该方程恒有一解;(2)当 时,
时, 恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是 ( )
恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是 ( )
A. B.
B. C.
C. D.
D.
第II卷(非选择题 共90分)
本卷包括必答题和选答题两部分。第13题-第21题为必答题,每个试题考生都必须作答。第22题-第24题为选答题,考生根据要求作答。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com