
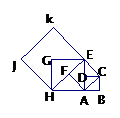
3. 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正
方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…
(1)记正方形ABCD的边长为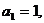 依上述方法所作的正方形的边长依次为
依上述方法所作的正方形的边长依次为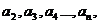
 求出
求出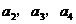 的值.
的值.
(2)根据以上规律写出第n个正方形的边长a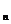 的表达式
的表达式
答案提示:
(1)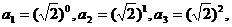
a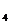 =(
=(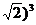 ;
;
(2)a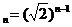 (n≧1的自然数)
(n≧1的自然数)
2. 如图所示的圆柱体中底面圆的半径是 4/π,高为3,若一只小虫从A点出发沿着圆柱的侧面
爬行到点C,则小虫爬行的最短路程是 . 答案:5

例4. 已知直角三角形的两边长分别为5和12,求第三边长.
分析:已知直角三角形的两边的长度,并没有指明哪一条边是斜边,因此要分类讨论.
解:(1)当5和12均是直角边时,则由勾股定理可得斜边的长度为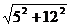 =13;
=13;
(2)当5是直角边,12是斜边时,则由勾股定理可得另一直角边长为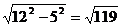 .
.
综合(1)、(2)得第三边的长为13或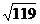 。
。
试一试(供同学们练习)
1.(2008年荆州市)如图所示的长方体是某种饮料的纸质包装盒,规格为5×6×10(单位:㎝),
在上盖中开有一孔便于插吸管,吸管长为13㎝, 小孔到图中边AB距离为1㎝,到上盖
中与AB相邻的两边距离相等,设插入吸管后露在盒外面的管长为h㎝,则h的最小值大约
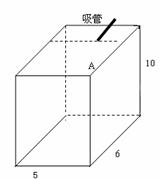 为_________㎝.(精确到个位)
为_________㎝.(精确到个位)
参考数据: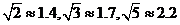 )
)
例3. 如图3,铁路上A、B两点相距25km,C、D两点为村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km。现在要在铁路AB上建一个农贸市场E,使得C、D两村到农贸市场E的距离相等,则农贸市场E应建在距A站多少km处?
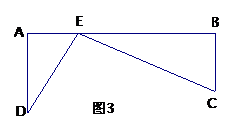
分析:这是一个实际生活中的问题,从图中可以看出,如果单独解直角三角形,这时条件不够,根据题意,不妨把两个直角三角形同时考虑进去,设未知数,如果设AE=x,结合勾股定理,抓住等量关系“DE=CE”列出方程就可以解决问题了。
解:设AE=x km,由勾股定理得,15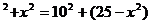
解此方程得 x=10
故农贸市场E应建在铁路上离A站10km处。
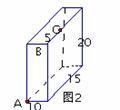 例2. 如图2,长方体的长为15cm,宽为10cm,高为20cm,点B离点C的距离是5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点C,需要爬行的最短路径是多少?
例2. 如图2,长方体的长为15cm,宽为10cm,高为20cm,点B离点C的距离是5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点C,需要爬行的最短路径是多少?
分析:蚂蚁实际上是在长方体的侧面上爬行,如果将长方体的侧面展开(如图2-1),根据“两点之间线段最短.” 所以求得的路径就是侧面展开图中线段AC之长,但展开方式有3种,这样通过侧面展开图把立体图形转化为平面图形,构造成直角三角形,利用勾股定理便可求解.
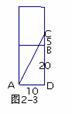
解:如图所示,把长方体展开后得到如图2-1、图2-2、图2-3三种情形,蚂蚁爬
 行的路径为展开图中的AC长,根据勾股定理可知:
行的路径为展开图中的AC长,根据勾股定理可知:
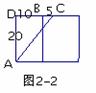
 在图2-1中,AC
在图2-1中,AC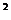 =AB
=AB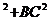 =30
=30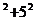 =925
=925
图2-2中, AC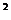 =AD
=AD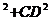 =20
=20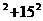 =625
=625
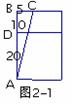
图2-3中, AC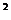 = AD
= AD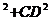 =25
=25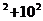 =725
=725
于是,根据上面三种展开情形中的AC长比较,最短的路径是在图2-2中,故蚂蚁从A点爬行到点C,最短距离为25cm.
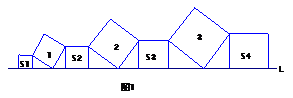 例1. 在直线L上依次摆放着七个正方形(如图1所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S
例1. 在直线L上依次摆放着七个正方形(如图1所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S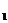 、S
、S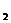 、S
、S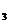 、S
、S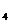 ,则S
,则S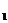 +S
+S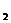 +S
+S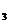 +S
+S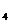 =
=
.
分析:经过观察图形,可以看出正放着正方形面积与斜放置的正方形之间关系为: S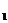 +S
+S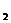 =1;S
=1;S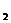 +S
+S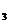 =2; S
=2; S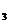 +S
+S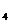 =3;这样数形结合可把问题解决.
=3;这样数形结合可把问题解决.
解: S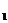 代表的面积为S
代表的面积为S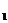 的正方形边长的平方, S
的正方形边长的平方, S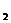 代表的面积为S
代表的面积为S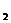 的正方形边长的平方,所以S
的正方形边长的平方,所以S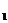 +S
+S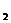 =斜放置的正方形面积为1;同理S
=斜放置的正方形面积为1;同理S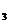 +S
+S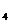 =斜放置的正方形面积为3,故S
=斜放置的正方形面积为3,故S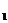 +S
+S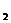 +S
+S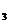 +S
+S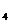 =1+3=4.
=1+3=4.
26. (1)设xs后,△PBQ的面积等于4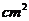 .
.
此时,AP=xcm,PB=(5-x)cm,BQ=2xcm.
由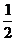 BP·BQ=4,得
BP·BQ=4,得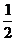 (5-x)·2x=4.
(5-x)·2x=4.
即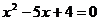 ,解得
,解得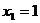 ,
,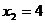 (不合题意思,舍去).
(不合题意思,舍去).
所以1s后,△PBQ的面积等于4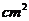 .
.
(2)仿(1),得,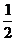 (5-x)·2x=7.
(5-x)·2x=7.
整理,得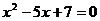 ,因为
,因为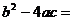 25-28<0,
25-28<0,
所以,此方程无解.
所以△PBQ的面积不可能等于7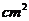 .
.
25. 7cm.
24. 设该单位这次共有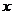 名员工去天水湾风景区旅游,因为
名员工去天水湾风景区旅游,因为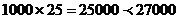 ,所以员工人数一定超过25人。 可得方程
,所以员工人数一定超过25人。 可得方程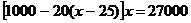
解得: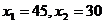 。
。
当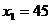 时,
时,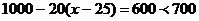 ,故舍去
,故舍去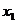
当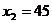 时,
时,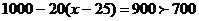 ,符合题意
,符合题意
答:该单位这次共有30名员工去天水湾风景区旅游。
23. 设每轮感染中平均一台电脑会感染x台电脑,则经过1轮后有(1+x)台被染上病毒,2轮后就有(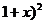 台被染毒,依题意,得
台被染毒,依题意,得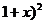 =81,解得
=81,解得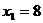 ,
,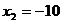 (舍去).
(舍去).
所以每轮感染中平均一台电脑会感染8台电脑.
由此规律,经过3轮后,有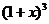 =
=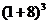 =729.
=729.
由于729>700, 所以若病毒得不到有效控制,3轮感染后,被感染的电脑会超过700台.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com