
3. 已知:如图2,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为 ( ).
(A)9
(B)3
(C)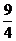 (D)
(D)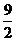
2. 如图1,直角三角形ABC的周长为24,且AB:BC=5:3,则AC= ( ).
(A)6 (B)8 (C)10 (D)12

1. 下列各组中,不能构成直角三角形的是 ( ).
(A)9,12,15 (B)15,32,39 (C)16,30,32 (D)9,40,41
例1(2009丽水市)如图1中,图①是一块边长为1,周长记为P1的正三角形纸板,沿图①的底边剪去一块边长为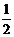 的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的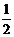 )后,得图③,④,…,记第n(n≥3) 块纸板的周长为Pn,则Pn-Pn-1=
▲
.
)后,得图③,④,…,记第n(n≥3) 块纸板的周长为Pn,则Pn-Pn-1=
▲
.

分析:本题是一道以等边三角形为情境的规律探究题,解答时关键是结合图形序号与图形中边长的长度之间变化的规律.
解:因为第②个图形中剪掉部分的边长为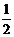 ;第③个图形中新剪掉的正三角形边长又是在第1次剪掉的正三角形边长的
;第③个图形中新剪掉的正三角形边长又是在第1次剪掉的正三角形边长的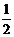 ,即得到剪掉的新正三角形边长为
,即得到剪掉的新正三角形边长为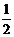 ×
×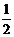 =
=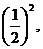 接下来第④个图形中被剪掉的正三角形边长为是第3次被剪掉的正三角形边长为
接下来第④个图形中被剪掉的正三角形边长为是第3次被剪掉的正三角形边长为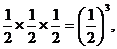 依次类推,第④个图形中新剪掉的新正三角形边长为
依次类推,第④个图形中新剪掉的新正三角形边长为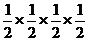 =
=
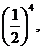 ….,第n个图形新剪掉的新正三角形边长为
….,第n个图形新剪掉的新正三角形边长为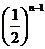 .可以看出后一个图形比前一个图形多出一个新正三角形,于是有
.可以看出后一个图形比前一个图形多出一个新正三角形,于是有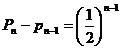 .
.
说明:本题目实际上相当于求连续两个图形中最后剪掉的正三角形的边长,规律探究题中,需要进行观察、猜想、分析、进行合情推理.
例4 (09毕节)在一次数学课上,汪老师在黑板上画出如图4,并写出了四个等式:
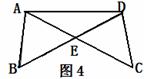 ①AB=DC
,②BE=CE,③∠B=∠C,④∠BAE=∠CCDE.
①AB=DC
,②BE=CE,③∠B=∠C,④∠BAE=∠CCDE.
要求同学们从这四个等式中选出两个作为条件,
推出△ADE是等腰三角形.请你试着完成汪老师提出的要求,
并说明理由.
分析:本题是一道等腰三角形的开放性试题,考查了
同学们综合运用所学知识判定等腰三角形的能力,由条件①③,或①④,或②③,或②④,均可证明△AED是等腰三角形,这里给出用①③为已知时△AED是等腰三角形的证明.
证明:在△ABE和△DCE中,
 ∴△ABE≌△DCE ∴AE=DE,即△AED是等腰三角形.
∴△ABE≌△DCE ∴AE=DE,即△AED是等腰三角形.
说明:本题颇有新意,提供了一种较新的考查方式,把传统的几何证明题,改造成一个学生发现、猜想、证明组合的开放型问题,符合课标精神,是近年中考的一个新亮点.
等腰三角形是中学数学的重要内容,也是中考的重要考点.特别是近年来与等腰三角形有关的考题新颖、富有创新.现进行例析如下,以便同学们参考.
例3 (2009襄樊市)在 中,
中,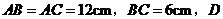 为
为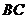 的中点,动点
的中点,动点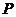 从
从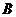 点出发,以每秒1
点出发,以每秒1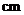 的速度沿
的速度沿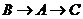 的方向运动.设运动时间为
的方向运动.设运动时间为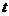 ,那么当
,那么当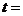 秒时,过
秒时,过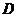 、
、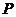 两点的直线将
两点的直线将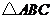 的周长分成两个部分,使其中一部分是另一部分的2倍.
的周长分成两个部分,使其中一部分是另一部分的2倍.
解析:本题考查等腰三角形中的动点问题,两种情况,①当点P在BA上时,BP=t,AP=12-t, 2(t+3)=12-t+12+3, 解得t=7; ②当点P在AC上时, PC=24-t,t+3
=2(24-t+3),解得t=17,故填7或17.
说明:动态型问题是近年中考的一个亮点,这是一道较为容易的动态问题,这类问题主要抓住不变的因素,以不变应多变,分析问题要冷静.
例1 (2009年黄冈市)在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为50°,则∠B等于_____________度.
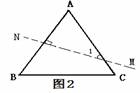 分析:本题是一道等腰三角形计算角度的分类讨论题,题目只要根据题意,画出等腰三角形腰与底边之间两种情形的图形进行分析即可解决.
分析:本题是一道等腰三角形计算角度的分类讨论题,题目只要根据题意,画出等腰三角形腰与底边之间两种情形的图形进行分析即可解决.
解:如图2,在等腰三角形ABC中,当腰AB与AC都
大于底边时,这时AB的垂直平分线MN与AC所在的直线相
交所得到锐角为50°,即∠1=50°.所以∠A=40°,于是
∠B=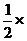 (180°-40°)=
(180°-40°)=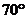 .
.
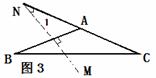 如图3,当腰AB与AC都小于BC时,这时AB的垂
如图3,当腰AB与AC都小于BC时,这时AB的垂
直平分线MN与AC所在的直线相交所成的角在△ABC外.
.即∠1=50°,所以∠BAC=90°+50°=140°.于是
∠B=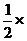 (180°-140°)=
(180°-140°)=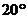 . 故填
. 故填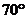 或
或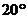 .
.
说明:等腰三角形的图形“肥瘦”与“矮胖”,往往在求角度或边的长时,要思维严谨,以防漏解现象.
例1(09镇江)如图1,两个全等的等边三角形的边长为1米,一个微型的机器
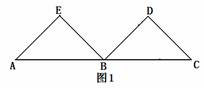 人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2010米停下,此时这个微型机器人停在( ).
人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2010米停下,此时这个微型机器人停在( ).
(A)A点 (B)B点
(C)C点 (D)D点
分析:本题是一道以等边三角形为情
境的规律探究题,题目中涉及到循环规律,根据等边三角形三边都相等,进一步找出循环规律.
解:由等边三角形的性质可知机器人每个循环的路程都是6米,而用2010米除以6,商正好是335,说明机器人走2010米正好进行了335个循环,所以不难判断机器人最后应停留在A点.
说明:解决关于循环规律问题,先根据特殊图形具有的性质找出具有规律性的周期,再利用周期计算出结论,从而达到“探究规律得到结论,运用结论妙解题”的目的.
13、下面一段文字中人物的语言有不得体之处.找出四处并加以修改。(4分)
王凯和李阳从小学到高中都是同班同宿舍同桌,十几年来一起长大,友谊深厚,高考后两人分别被两所高校录取。回校取录取通知书时,两人相见,王凯拉住李阳的手说: “李阳同学你好,今天与你在此幸会,我都高兴死了!咱俩青梅竹马,一起长大,你给了我很多的帮助。我永远感谢你,你有用得着我的地方,我也一定鼎力相助。希望今后我们保持联系。”
①将____________修改为___________ ②将____________修改为____________
③将____________修改为___________ ④将____________修改为____________
[答案]①李阳同学--阳子(或:李阳) ②幸会--相见(或:相聚) ③青梅竹马--(应该删去) ④鼎力相助--全力帮忙(每点1分,共4分。顺序不论。)
[解析]解题的重点是要注意说话人的身份及其关系。语段中是两位亲密的高中同学,加以场合的考虑,语言表达不应该过于客气和隆重。[易错考点二]得体
12、 “春蕾文学社”要举办一场“读名著、谈感受”报告会,请你为主持人设计一则开场白。要求:彰显主题,巧用修辞,语言有文采。开场白的思路要求是:名著是……名著是……读名著……读名著……(100字以内)(4分)
[答案]示例:名著是历史天空中璀璨的星辰,凝聚着前人智慧的光芒;名著是岁月长河中晶莹的水滴,折射着时代动人的光彩。读名著是和渊博的智者交谈,读名著是站在巨人的肩上眺望。春蕾文学社“读名著、谈感受”报告会正式开始!(内容2分,形式2分。)
[解析]此题考查多个知识点,其中重要的一个知识点就是得体。这体现在三方面:其一是对名著的认识和界定,其二是表达读名著的意义,其三是要符合开场白的语言要求。[易错考点二]得体
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com