
19.(本小题满分16分)
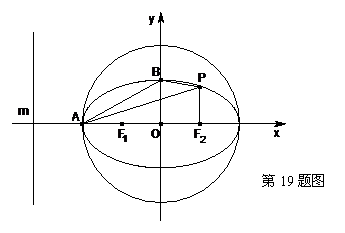
如图,已知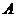 ,
,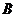 是中心在原点
是中心在原点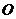 ,焦点在
,焦点在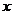 轴上,离心率
轴上,离心率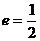 的椭圆的左顶点和上顶点,
的椭圆的左顶点和上顶点,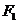 ,
,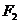 是左、右焦点,点
是左、右焦点,点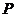 在椭圆上,且在
在椭圆上,且在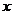 轴上方,
轴上方,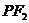 垂直于
垂直于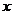 轴,
轴,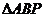 的面积为
的面积为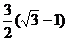 .
.
(1)求椭圆方程;
(2)我们把以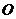 为圆心,
为圆心, 为半径的圆称为“椭圆的大圆”.若直线
为半径的圆称为“椭圆的大圆”.若直线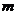 是椭圆的左准线,
是椭圆的左准线,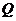 是直线
是直线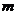 上一动点,以
上一动点,以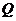 为圆心,且经过
为圆心,且经过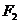 的圆与该椭圆的大圆相交于
的圆与该椭圆的大圆相交于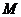 ,
, 两点,求证:直线
两点,求证:直线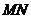 过一定点,并求出定点坐标;
过一定点,并求出定点坐标;
 (3)在(2)中,若将条件“直线
(3)在(2)中,若将条件“直线 是椭圆的左准线”改为“直线
是椭圆的左准线”改为“直线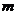 过
过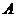 点且平行于椭圆的准线”,是否有类似的结论?根据你的推理,给出一个更为一般的结论(无需证明).
点且平行于椭圆的准线”,是否有类似的结论?根据你的推理,给出一个更为一般的结论(无需证明).
18.(本小题满分15分)
已知命题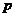 :函数
:函数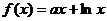 (
(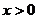 )存在单调减区间;命题
)存在单调减区间;命题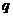 :函数
:函数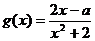 在区间
在区间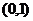 上是增函数.若
上是增函数.若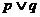 是真命题,
是真命题,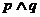 是假命题,求实数
是假命题,求实数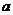 的取值范围.
的取值范围.
17.(本小题满分15分)
为了配合某项问卷调查,决定抽取 3个学生参加,且名额要从高二(1),(2),(3)三个班学生中随机抽取.(说明:每个班的总人数均不少于3人)
(1)求抽取出来的3个学生全部来自同一个班级的概率;
(2)求抽取出来的3个学生所在班级均不相同的概率;
(3)至少有2人来自同一个班级的概率.
16. (本小题满分14分)
(1)已知抛物线的顶点在原点,对称轴为坐标轴,焦点在直线 上,求抛物线的标准方程;
上,求抛物线的标准方程;
(2)若双曲线经过点(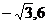 ),且它的两条渐近线方程是
),且它的两条渐近线方程是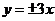 ,求此双曲线的标准方程.
,求此双曲线的标准方程.
15.(本小题满分14分)
某校高一年级开设了“校园植物”的校本课程,该班同学利用课余时间,对学校的树木底部直径d(单位:cm)作了抽样调查,并将调查结果统计成下表:
|
直径 |
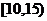 |
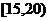 |
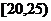 |
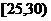 |
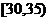 |
合计 |
|
棵数 |
20 |
5 |
15 |
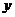 |
5 |
50 |
|
频率 |
0.40 |
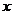 |
0.30 |
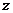 |
0.10 |
1 |
(1)计算表中的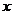 、
、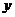 、
、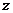 的值;
的值;
(2)估计该学校树木底部直径小于25cm的百分比;
(3)用各组区间的组中值估计该学校树木底部直径的平均值.
14.已知点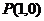 ,过点
,过点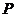 的直线
的直线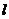 交抛物线
交抛物线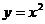 于
于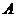 ,
,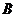 两点,且
两点,且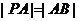 ,则直线
,则直线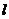 的斜率是 ▲
.
的斜率是 ▲
.
13.关于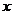 的方程
的方程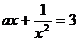 有且仅有一个实根,且根大于0,则实数
有且仅有一个实根,且根大于0,则实数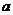 的取值范围
的取值范围
是 ▲ .
12.设e1、e2分别为两椭圆的离心率,则e1+e2>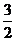 的概率为 ▲ .
的概率为 ▲ .
11.函数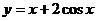 在区间
在区间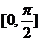 上的最大值是
▲ .
上的最大值是
▲ .
10.某单位一科室共有4名成员,现有2张2010年上海世博会门票供分配,且每人至多分得一张票.则该科室中,甲、乙二人至少有一人分到门票的概率是 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com