
10.已知奇函数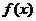 的定义域为R,且是以2为周期的周期函数,数列
的定义域为R,且是以2为周期的周期函数,数列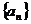 是首项为1,公
是首项为1,公
差为1的等差数列,则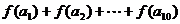 的值为
( A
)
的值为
( A
)
A.0 B.1 C.-1 D.2
9. a,b,c均为正数且表示线段长度,则a,b,c能构成锐角三角形的充要条件是(D )A.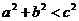 B.
B.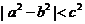
C.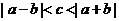 D.
D.
8.
若直线y=kx+2与双曲线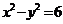 的右支交于不同的两点,则k的取值范围是(D )
的右支交于不同的两点,则k的取值范围是(D )
A. ,
,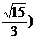 B.
B.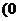 ,
,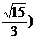 C.
C.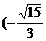 ,
,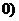 D.
D.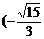 ,
,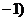
7.若M是直线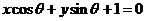 上到原点的距离最近的点,则当
上到原点的距离最近的点,则当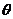 在实数范围内变化时,动点M的轨迹是
( C)
在实数范围内变化时,动点M的轨迹是
( C)
A.直线 B.线段 C.圆 D.椭圆
6. 已知三棱锥S-ABC中,SA,SB,SC两两互相垂直,底面ABC上一点P到三个面SAB,SAC,SBC的距离分别为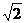 ,1,
,1, ,则PS的长度为
( D)
,则PS的长度为
( D)
A.9 B. C.
C.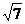 D.3
D.3
5.当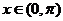 时,函数
时,函数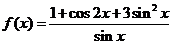 的最小值为
(B )
的最小值为
(B )
A.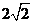 B.
B. C.
C.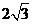 D.
D.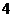
4.设等差数列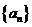 的前n项的和是Sn,且
的前n项的和是Sn,且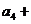
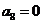 ,则 ( D)
,则 ( D)
A.S4<S5 B.S4=S5 C.S6<S5 D.S6=S5
3.在检查产品尺寸过程中,将其尺寸分成若干组,[a,b)是其中一组,抽查出的个体在该组上频率为m,该组上的直方图的高为h,则|a-b|= (B )
A、hm B、 C、
C、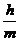 D、h+m
D、h+m
1.全集设为U,P、S、T均为U的子集,若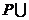 (
(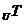 )=(
)=(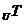 )
)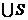 则
(A )
则
(A )
A.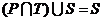 B.P=T=S C.T=U D.
B.P=T=S C.T=U D.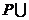 (
( )=T
)=T
2 与命题“若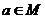 则
则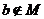 ”的等价的命题是 ( D )
”的等价的命题是 ( D )
A.若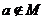 ,则
,则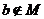 B.若
B.若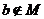 ,则
,则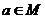
C.若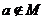 ,则
,则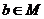 D.若
D.若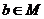 ,则
,则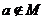
18.(1)证法1:∵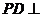 平面
平面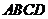 ,
,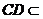 平面
平面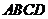 ,∴
,∴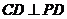 .
.
又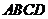 为正方形,∴
为正方形,∴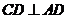 .∵
.∵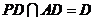 ,∴
,∴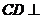 平面
平面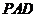 .
.
∵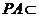 平面
平面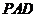 ,∴
,∴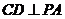 .∵
.∵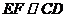 ,∴
,∴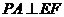 .
.
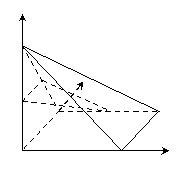
证法2:以 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系 ,
,
则 ,
,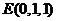 ,
,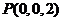 ,
,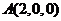 ,
,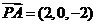 ,
,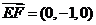 .
.
 ∵
∵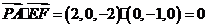 ,∴
,∴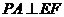 .
.
(2)解法1:以 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系 ,
,
则 ,
, ,
,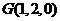 ,
,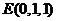 ,
,
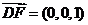 ,
,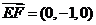 ,
,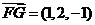 .
.
设平面DFG的法向量为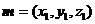 ,∵
,∵
令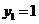 ,得
,得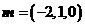 是平面
是平面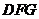 的一个法向量.
的一个法向量.
设平面EFG的法向量为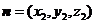 ,∵
,∵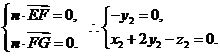
令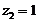 ,得
,得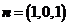 是平面
是平面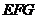 的一个法向量.
的一个法向量.
∵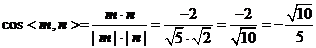 .
.
设二面角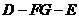 的平面角为θ,则
的平面角为θ,则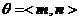 .
.
所以二面角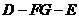 的余弦值为
的余弦值为 .
.
解法2:以 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系 ,
,
则 ,
, ,
,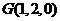 ,
,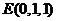 ,
,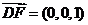 ,
,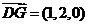 ,
,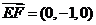 ,
,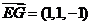 ,
,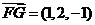 .………………………………8分
.………………………………8分
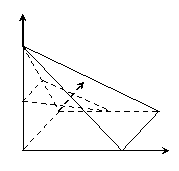 过
过 作
作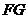 的垂线,垂足为
的垂线,垂足为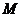 ,
,
∵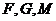 三点共线,∴
三点共线,∴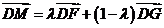 ,
,
∵ ,∴
,∴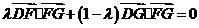 ,
,
即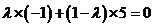 ,解得
,解得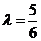 .
.
∴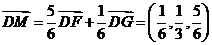 .…………10分
.…………10分
再过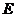 作
作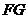 的垂线,垂足为
的垂线,垂足为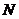 ,
,
∵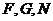 三点共线,∴
三点共线,∴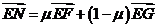 ,
,
∵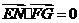 ,∴
,∴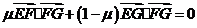 ,
,
即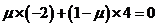 ,解得
,解得 .
.
∴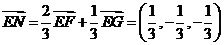 .∴
.∴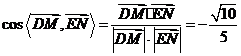 .
.
∵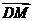 与
与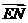 所成的角就是二面角
所成的角就是二面角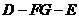 的平面角,
的平面角,
所以二面角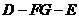 的余弦值为
的余弦值为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com