
5.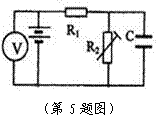 在温控电路中,通过热敏电阻阻值随温度的变化可实现对电路相关物理量的控制作用,如图所示电路,
在温控电路中,通过热敏电阻阻值随温度的变化可实现对电路相关物理量的控制作用,如图所示电路,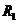 为定值电阻,
为定值电阻,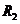 为半导体热敏电阻(温度越高电阻越小),C为电容器,当环境温度降低时 ( )
为半导体热敏电阻(温度越高电阻越小),C为电容器,当环境温度降低时 ( )
A.电压表的读数减小
B.电容器C的带电量增大
C.电容器C两板间的电场强度减小
D.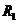 消耗的功率增大
消耗的功率增大
4.下列有关说法中正确的是 ( )
|
B.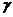 射线一般伴随着
射线一般伴随着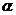 或
或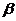 射线产生,在这三种射线中,
射线产生,在这三种射线中,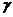 射线的穿透能力最强,电离能力也最强
射线的穿透能力最强,电离能力也最强
C.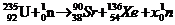 是核裂变方程,其中x=11
是核裂变方程,其中x=11
D.199F+11H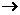 168O+42He是α衰变方程
168O+42He是α衰变方程
3.用一根长1m的轻质细绳将一副质量为1kg的画框对称悬挂在墙壁上,已知绳能承受的最大张力为10N,为使绳子不被拉断,画框上两个挂钉的间距最大为 ( )
 A.
A.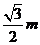 B.
B.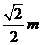
C.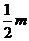 D.
D.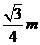
2.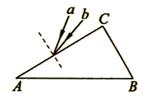 如图所示,两束单色光a、b分别照射到玻璃三棱镜AC面上
如图所示,两束单色光a、b分别照射到玻璃三棱镜AC面上
的同一点,且都垂直AB边射出三棱镜,则下列说法中正确
的是 ( )
A.a光的频率高
B.b光的波长大
|
D.b光穿过三棱镜的时间短
1.下列叙述中,符合物理学史事实的是 ( )
A.伽利略通过理想斜面实验,得出力不是维持物体运动原因的结论。
B.牛顿通过实验测出了万有引力常量,验证了万有引力定律。
C.贝克勒尔通过对天然放射性的研究,发现原子核是由质子和中子组成的。
D.汤姆孙预言了中子的存在,查德威克通过原子核人工转变的实验发现了中子。
8.[提示或答案]
解(1)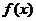 是奇函数,则
是奇函数,则
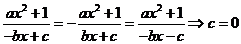 由
由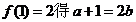 ,
,
由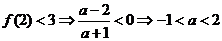
又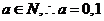 .
.
当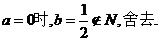
当a=1时,b=1,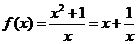
[基础知识聚焦]结合具体函数,考查函数性质
9[提示或答案]
分析:欲证f(x)为奇函数即要证对任意x都有f(-x)=-f(x)成立.在式子f(x+y)=f(x)+f(y)中,令y=-x可得f(0)=f(x)+f(-x)于是又提出新的问题,求f(0)的值.令x=y=0可得f(0)=f(0)+f(0)即f(0)=0,f(x)是奇函数得到证明.
(1)证明:
f(x+y)=f(x)+f(y)(x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,则有
0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,所以f(x)是奇函数.
(2)解:f(3)=log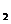 3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.
3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.
f(k·3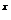 )<-f(3
)<-f(3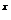 -9
-9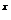 -2)
-2)
=f(-3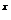 +9
+9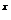 +2),
+2),
k·3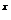 <-3
<-3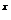 +9
+9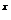 +2,
+2,
3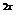 -(1+k)·3
-(1+k)·3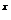 +2>0对任意x∈R都成立.令t=3
+2>0对任意x∈R都成立.令t=3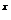 >0,问题等价于t
>0,问题等价于t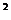 -(1+k)t+2>0对任意t>0恒成立.
-(1+k)t+2>0对任意t>0恒成立.
令f(t)=t2-(1+k)t+2,其对称轴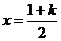
当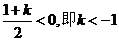 时,f(0)=2>0,符合题意;
时,f(0)=2>0,符合题意;
当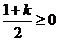 时,对任意t>0,f(t)>0恒成立
时,对任意t>0,f(t)>0恒成立
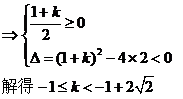
综上所述,所求k的取值范围是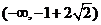
[基础知识聚焦]考查奇偶性解决抽象函数问题,使学生掌握方法。
10[提示或答案]B
11[提示或答案]D
12[提示或答案]D
[基础知识聚焦]掌握奇偶函数的性质及图象特征
13[提示或答案]6
[基础知识聚焦]考查奇偶性及整体思想
[变式与拓展]:f(x)=ax3+bx-8,且f(-2)=10,则f(2)=_____________。
14[提示或答案]由f(0)=0得a=1
[基础知识聚焦]考查奇偶性。若奇函数f(x)的定义域包含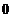 ,则f(0)=0;
,则f(0)=0;
f(x)为偶函数óf(x)=f(|x|)
15[提示或答案]画图可知,解集为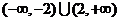 ;
;
16[提示或答案]x<-1,0<x<1
17[提示或答案](1)偶函数 (2)x>0时,f(x)>0,x<0时-x>0,f(x)=f(-x)>0
7. [提示或答案]
-1<1-a<1
-1<1-a2<1
f(1-a)<- f(1-a2)=f(a2-1),1-a> a2-1得0<a<1
[基础知识聚焦]考查奇偶性解决抽象函数问题
6.解:设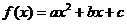 则
则
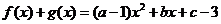 是奇函数
是奇函数
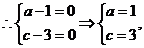
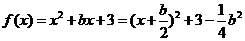
(1)当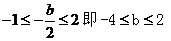 时,最小值为:
时,最小值为: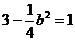
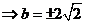
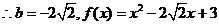
(2)当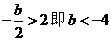 时,f(2)=1无解;
时,f(2)=1无解;
(3)当 时,
时,
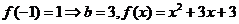
综上得: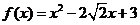 或
或 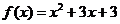
[基础知识聚焦]利用函数性质求函数解析式,渗透数形结合
5.[提示或答案]
解(1)此函数的定义域为R.
∵f(-x)+f(x)=lg(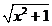 +x)+lg(
+x)+lg(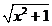 -x)=lg1=0
-x)=lg1=0
∴f(-x)=-f(x),即f(x)是奇函数。
(2)此函数定义域为{2},故f(x)是非奇非偶函数。
(3)∵函数f(x)定义域(-∞,0)∪(0,+∞),当x>0时,-x<0,
∴f(-x)=(-x)[1-(-x)]=-x(1+x)=-f(x)(x>0).
当x<0时,-x>0,∴f(-x)=-x(1-x)=-f(x)(x<0).
故函数f(x)为奇函数.
[基础知识聚焦]考查奇偶性的概念并会判断函数的奇偶性
4. [提示或答案]f(x)=-x-x4
[变式与拓展]已知f(x)是定义在R上的奇函数,x>0时,f(x)=x2-2x+3,则f(x)=________________。
[基础知识聚焦]利用函数性质求函数解析式
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com