
9.在用插针法测定玻璃砖折射率的实验中,甲、乙、丙三位同学在纸上画出的界面aa′、bb′与玻璃砖位置的关系分别如图实14-14①、②和③所示,其中甲、丙两同学用的是矩形玻璃砖,乙同学用的是梯形玻璃砖.他们的其它操作均正确,且均以aa′、bb′为界面画光路图,则( )
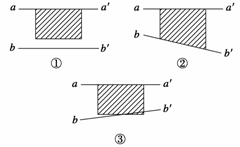
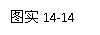
甲同学测得的折射率与真实值相比 (填“偏大”“偏小”或“不变”).
乙同学测得的折射率与真实值相比 (填“偏大”“偏小”或“不变”).
丙同学测得的折射率与真实值相比 .
8. 如图实14-13所示,一个学生按照课本上的小实验用广口瓶和直尺测定水的折射率,填写下述实验步骤中的空白.
如图实14-13所示,一个学生按照课本上的小实验用广口瓶和直尺测定水的折射率,填写下述实验步骤中的空白.
(1)用__________测出广口瓶瓶口的内径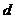 ;
;
 (2)在瓶内装满水;
(2)在瓶内装满水;
(3)将直尺沿瓶口边缘__________插入水中;
(4)沿广口瓶边缘向水中直尺正面看去,若恰能看到直尺的0刻度(即图中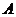 点),
点),
同时看到水面上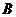 点刻度的像恰与
点刻度的像恰与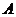 点的像相重合;
点的像相重合;
(5)若水面恰与直尺的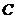 点相平,读出__________和__________的长度;
点相平,读出__________和__________的长度;
(6)以题中所给的条件为依据,计算水的折射率为__________.
7.某同学由于没有量角器,他在完成了光路图以后,以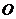 点为圆心、10.00 cm长为半径
点为圆心、10.00 cm长为半径
画圆,分别交线段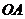 于
于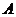 点,交
点,交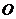 、
、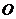 ′连线延长线于
′连线延长线于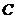 点.过
点.过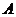 点作法线
点作法线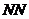 ′的
′的
垂线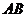 交
交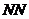 ′于
′于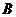 点,过
点,过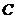 点作法线
点作法线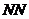 ′的垂线
′的垂线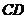 交
交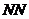 ′于
′于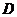 点,
点,
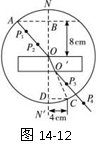
如图实14-12所示.用刻度尺量得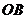 =8.00 cm,
=8.00 cm, 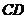 =4.00 cm.由此可得出玻璃
=4.00 cm.由此可得出玻璃
折射率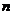 =___________.
=___________.
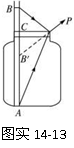
6.某校开展研究性学习,某研究小组根据光学知识,设计了一个测液体折射率的仪器.如图实14-11,在一个圆盘上,过其圆心O作两条相互垂直的直径BC、EF.在半径OA上,垂直盘面插上两枚大头针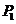 、
、 并保持位置不变.每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察
并保持位置不变.每次测量时让圆盘的下半部分竖直进入液体中,而且总使得液面与直径BC相平,EF作为界面的法线,而后在图中右上方区域观察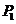 、
、 .同学们通过计算,
.同学们通过计算,
预先在圆周EC部分刻好了折射率的值,这样只要根据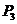 所插的位置,就可以直接读出
所插的位置,就可以直接读出
液体折射率的值.
(1)若∠AOF=30°,OP3与OC之间的夹角为30°,则P3处刻的折射率的值 .
(2)图中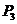 、
、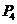 那一处对应的折射率大?
那一处对应的折射率大?
(3)做AO的延长线交圆周于K,K处对应的折射率为 .

5.如图实14-10所示,是利用插针法测定玻璃砖的折射率的实验得到的光路图.玻璃砖的入射面AB和出射面CD并不平行,则
(1)出射光线与入射光线 .(填仍平行或不再平行).
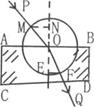 (2)以入射点O为圆心,以R=5cm长度为半径画圆,与入射线PO交于M点,与折射线OQ交于F点,过M、F点分别向法线作垂线,量得Mn=1.68cm,EF=1.12cm,则该玻璃砖的折射率n=
(2)以入射点O为圆心,以R=5cm长度为半径画圆,与入射线PO交于M点,与折射线OQ交于F点,过M、F点分别向法线作垂线,量得Mn=1.68cm,EF=1.12cm,则该玻璃砖的折射率n=

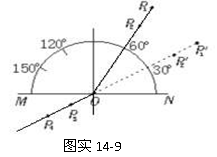
4.如图实14-9所示:一半圆形玻璃砖外面插上 、
、 、
、 、
、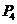 四枚大头针时,
四枚大头针时,
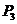 、
、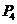 恰可挡住
恰可挡住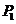 、
、 所成的像,则该玻璃砖的折射率
所成的像,则该玻璃砖的折射率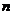 =______.有一同学
=______.有一同学
把大头针插在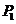 ′、
′、 ′位置时,沿着
′位置时,沿着
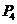 、
、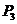 的方向看不到大头针的像,其原因是_______________________.
的方向看不到大头针的像,其原因是_______________________.
A 基础达标
1.测定玻璃的折射率时,为了减小实验误差,应该注意的是( )
A.玻璃砖的宽度应大些
B.入射角应尽量小些
C.大头针应垂直地插在纸面上
D.大头针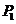 、
、 及
及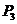 、
、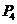 之间的距离应适当大些
2.某同学用插针法测定玻璃的折射率n,如图实14-7所示,他的实验方法和操作步骤正确无误,但事后发现玻璃砖的两个光学面
之间的距离应适当大些
2.某同学用插针法测定玻璃的折射率n,如图实14-7所示,他的实验方法和操作步骤正确无误,但事后发现玻璃砖的两个光学面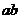 与
与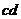 不平行.那么下列说法正确的是( )
不平行.那么下列说法正确的是( )
 A.
A. 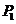 、
、 与
与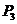 、
、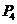 两条直线一定不平行
两条直线一定不平行
B. 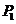 、
、 与
与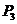 、
、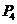 两条直线一定平行
两条直线一定平行
C.他测出的 值一定偏大
值一定偏大
D.他测出的 值不受影响
值不受影响
3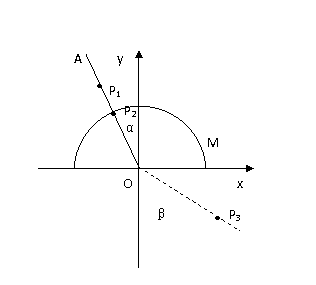 .如图实14-8,画有直角坐标系Oxy的白纸
.如图实14-8,画有直角坐标系Oxy的白纸
位于水平桌面上,M是放在白纸上的半圆
形玻璃砖,其底面的圆心在坐标的原点,直
边与x轴重合,OA是画在纸上的直线,
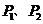 为竖直地插在直线OA上的两枚大
为竖直地插在直线OA上的两枚大
头针,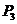 是竖直地插在纸上的第三枚大头针,
是竖直地插在纸上的第三枚大头针,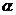 是直线OA与y轴正方向的夹角,
是直线OA与y轴正方向的夹角,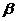
是直线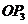 与轴负方向的夹角,只要直线OA画得合适,且
与轴负方向的夹角,只要直线OA画得合适,且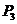 的位置取得正确,测得角
的位置取得正确,测得角
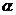 和
和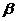 ,便可求得玻璃得折射率。
,便可求得玻璃得折射率。
某学生在用上述方法测量玻璃的折射率,在他画出的直线OA上竖直插上了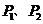 两枚大头针,但在y<0的区域内,不管眼睛放在何处,都无法透过玻璃砖看到
两枚大头针,但在y<0的区域内,不管眼睛放在何处,都无法透过玻璃砖看到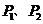 的像,他应该采取的措施是_____________________________________________________________
的像,他应该采取的措施是_____________________________________________________________
_________________________________________________________________.若他已透过玻璃砖看到了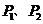 的像,确定
的像,确定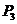 位置的方法是____________________________________
位置的方法是____________________________________
_________________________________________.若他已正确地测得了的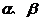 的值,则玻璃的折射率n=_____________________________.
的值,则玻璃的折射率n=_____________________________.
(四)、误差来源及分析
1.确定入射光线和出射光线时存在误差.
2.测量入射角和折射角时存在测量误差.
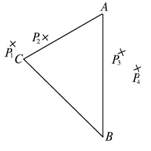 [例题]用三棱镜测定玻璃折射率的实验中,先在白纸上放好三棱镜,在棱镜的一侧插上两枚大头针P1和P2.然后在棱镜的另一侧观察,调整视线使P1的像被P2挡住,接着在眼睛所在的一侧插两枚大头针P3和P4,使P3挡住P1、P2的像,P4挡住P3和P1、P2的像.在纸上标出的大头针位置和三棱镜轮廓如图所示。
[例题]用三棱镜测定玻璃折射率的实验中,先在白纸上放好三棱镜,在棱镜的一侧插上两枚大头针P1和P2.然后在棱镜的另一侧观察,调整视线使P1的像被P2挡住,接着在眼睛所在的一侧插两枚大头针P3和P4,使P3挡住P1、P2的像,P4挡住P3和P1、P2的像.在纸上标出的大头针位置和三棱镜轮廓如图所示。
 (1)在本题的图14-4上画出所需的光路;
(1)在本题的图14-4上画出所需的光路;
 (2)为了测出棱镜玻璃的折射率,需要测量的量是__________和__________,在图上标出它们;
(2)为了测出棱镜玻璃的折射率,需要测量的量是__________和__________,在图上标出它们;
(3)计算折射率的公式是n=__________。
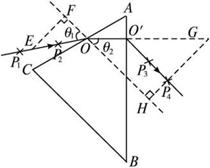
(1)如图实14-5所示,画出通过P1和P2、P3和P4的光线,分别与AC、AB边交于O、O′点,连结OO′。
 (2)过O点作AC的法线,标明入射角θ1和折射角θ2,并画出虚线部分,测出入射角θ1和折射角θ2(或线段EF、OE、GH、OG的长度)。
(2)过O点作AC的法线,标明入射角θ1和折射角θ2,并画出虚线部分,测出入射角θ1和折射角θ2(或线段EF、OE、GH、OG的长度)。
(3)n=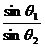 (或n=
(或n=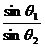 =
=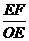 /
/ =
= ·
·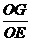 ,若作图时取OG=OE,则n=
,若作图时取OG=OE,则n= ,可以简化计算)。
,可以简化计算)。
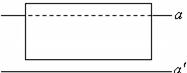 [变式训练]用两面平行的玻璃砖测定玻璃折射率的实验中,某同学画好玻璃砖的界面
[变式训练]用两面平行的玻璃砖测定玻璃折射率的实验中,某同学画好玻璃砖的界面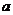 和
和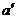 后,实验过程中不慎将玻璃砖向上平移了一些,如图实14-6所示,而实验的其它操作均正确,则测得的折射率将( )
后,实验过程中不慎将玻璃砖向上平移了一些,如图实14-6所示,而实验的其它操作均正确,则测得的折射率将( )
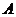 .偏大
.偏大
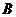 .偏小
.偏小
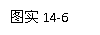
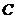 .不变
.不变

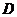 .无法确定
.无法确定
解析:该同学确定好了四枚大头针的位置以后,把玻璃砖移走,是按原来画好的两个界面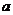 和
和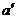 作光路图的,如图实14-7所示,入射点为
作光路图的,如图实14-7所示,入射点为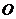 ,出射点为
,出射点为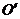 ,即他认为玻璃砖内的折射光线是
,即他认为玻璃砖内的折射光线是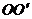 。而由于做实验过程中,把玻璃砖线上平移到了如图所示的位置上,入射到玻璃砖上表面的光线其实在玻璃砖上表面的
。而由于做实验过程中,把玻璃砖线上平移到了如图所示的位置上,入射到玻璃砖上表面的光线其实在玻璃砖上表面的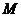 点就发射了折射,玻璃砖内的折射光线其实是沿
点就发射了折射,玻璃砖内的折射光线其实是沿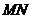 方向的,出射点为
方向的,出射点为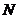 。由几何知识可以证明,
。由几何知识可以证明,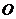 、
、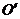 、
、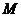 和
和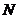 四个点正好构成一个平行四边形,即
四个点正好构成一个平行四边形,即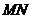 和
和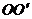 是平行的,则对于玻璃砖折射率的计算结果是没有影响的,所以答案为
是平行的,则对于玻璃砖折射率的计算结果是没有影响的,所以答案为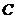 。
。
命题解读:这其实就是一个实验误差的分析问题,用到了光的折射和几何知识。同样的方法可以分析,放置玻璃砖时如果倾斜了,误差将会是怎样的?
(三)、其他数据处理方法
此实验是通过测量入射角和折射角,然后查数学用表,找出入射角和折射角的正弦值,再代人 中求玻璃的折射率.除运用此方法之外,还有以下处理数据的方法:
中求玻璃的折射率.除运用此方法之外,还有以下处理数据的方法:
1. 在找到人射光线和折射光线以后,以入射点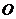 为圆心,以任意长为半径画圆,
为圆心,以任意长为半径画圆,
分别与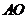 交于
交于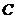 点,与
点,与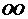 ’(或
’(或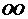 ’的延长线)交于
’的延长线)交于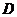 点,过
点,过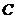 、
、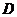
两点分别向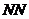 ’作垂线,交
’作垂线,交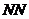 ’于
’于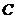 ’、
’、 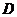 ’,用直尺量出
’,用直尺量出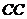 ’和
’和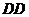 ’
’
的长.如图14-3-3所示.
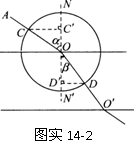 由于
由于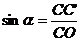 ,
, 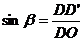
而CO=DO,所以折射率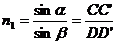
重复以上实验,求得各次折射率计算值,然后求其平均值即为玻璃砖折射率的测量值.
2.根据折射定律可得

因此有 
在多次改变入射角、测量相对应的入射角和折射角正弦值基础上,
以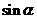 值为横坐标,以
值为横坐标,以 值为纵坐标建立直角坐标系.如图实14-3所示.
值为纵坐标建立直角坐标系.如图实14-3所示.
 描数据点,过数据点连线得一条过原点的直线.
描数据点,过数据点连线得一条过原点的直线.
求解图线斜率,设斜率为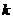 ,则
,则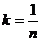 .
.
故玻璃砖折射率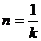
(二)、注意事项:
1.实验时,尽可能将大头针竖直插在纸上,且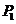 和
和 之间、
之间、 与
与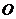 点之间、
点之间、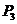 与
与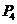 之间、
之间、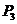 与
与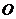 ’之间距离要稍大一些.
’之间距离要稍大一些.
2.入射角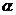 应适当大一些,以减小测量角度的误差.但入射角不宜太大,也不宜太小.
应适当大一些,以减小测量角度的误差.但入射角不宜太大,也不宜太小.
3.在操作时,手不能触摸玻璃砖的光洁光学面.更不能用玻璃砖界面代替直尺画界线.
4.在实验过程中,玻璃砖与白纸的相对位置不能改变.
5.玻璃砖应选用宽度较大的,宜在5cm以上.若宽度太小,则测量误差较大.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com