
1、关于一列简谐波,下面说法中正确的是[ ]
A.波动的产生需要两个条件,即波源和传播波的介质
B.波动过程是质点由近向远传递的过程
C.波动过程是能量传递的过程
D.波动过程中质点本身随波迁移
10.碰撞与反冲
例题17.质量相等的 、
、 两个小球在光滑的水平面沿同一直线、同方向运动,
两个小球在光滑的水平面沿同一直线、同方向运动, 、
、 两球的动量分别是
两球的动量分别是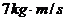 和
和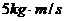 ,当
,当 球追上
球追上 球发生碰撞,则碰撞后
球发生碰撞,则碰撞后 、
、 两球动量的可能值是
两球动量的可能值是
 .
.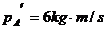 ,
,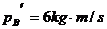
 .
.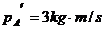 ,
,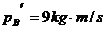
 .
.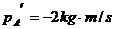 ,
,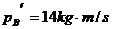
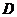 .
.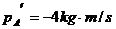 ,
,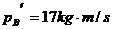
解析:发生碰撞的 、
、 两个小球在水平方向上不受外力作用,故
两个小球在水平方向上不受外力作用,故 、
、 两个小球组成的系统动量守恒,从题中的已知条件来看,作用前系统的总动量为
两个小球组成的系统动量守恒,从题中的已知条件来看,作用前系统的总动量为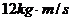 ,所以仅从这个角度看,题中的四个选项中只有
,所以仅从这个角度看,题中的四个选项中只有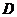 是错误的;再从另一角度讲,除爆炸类外,两个相互作用的物体的总能量是不会增加的,根据动能和动量的关系式
是错误的;再从另一角度讲,除爆炸类外,两个相互作用的物体的总能量是不会增加的,根据动能和动量的关系式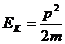 可知,
可知, 、
、 两个小球碰撞前的总动能为
两个小球碰撞前的总动能为 ,所以从这个角度判断,剩下的
,所以从这个角度判断,剩下的 、
、 和
和 三个选项中,只有
三个选项中,只有 是正确的。
是正确的。
故,答案为 。
。
命题解读:碰撞类问题有如下的三个特点:
①相互作用的时间极短,且作用力很大(远远大于系统所受的外力),故均可按动量守恒定律来处理,即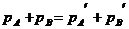 。
。
②碰撞后系统的总动能不会增加,即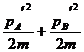 ≤
≤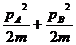 。
。
③若碰撞后两小球在一条直线上同方向运动,则一定是后一小球的运动速度不能大于前一小球的运动速度,否则碰撞就没有结束。
所以,对碰撞问题的分析和判断,一定要同时把握住以上的几个特点,决不能片面地以其中的一个或两个特点判断就得出结论。
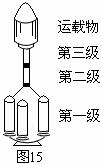 例题18.如图15是多级火箭的示意图,发射时先点燃第一级火箭,燃料燃烧完后,空壳自动脱落,然后下一级火箭开始工作,多级火箭能及时把空壳抛掉,使质量减小,因而能达到很高的速度,可用来发射洲际导弹、人造卫星和宇宙飞船等。试通过计算说明:火箭不是一次把燃气喷完,而是逐渐向后喷气以获得更大反冲速度的道理。(每次喷出的气体相对于火箭的速度是相同的,设火箭的运动方向为正方向,则喷出气体相对于地的速度
例题18.如图15是多级火箭的示意图,发射时先点燃第一级火箭,燃料燃烧完后,空壳自动脱落,然后下一级火箭开始工作,多级火箭能及时把空壳抛掉,使质量减小,因而能达到很高的速度,可用来发射洲际导弹、人造卫星和宇宙飞船等。试通过计算说明:火箭不是一次把燃气喷完,而是逐渐向后喷气以获得更大反冲速度的道理。(每次喷出的气体相对于火箭的速度是相同的,设火箭的运动方向为正方向,则喷出气体相对于地的速度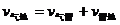 )
)
解析:设运载物的质量为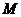 ,每一级火箭燃料及空壳的总质量为
,每一级火箭燃料及空壳的总质量为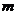 ,燃料相对于运载物的速度为
,燃料相对于运载物的速度为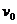 。
。
若三级火箭一次把燃料喷完,设运载物获得的速度为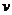 ,则由动量守恒定律得
,则由动量守恒定律得
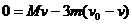
所以 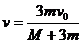
若三级火箭逐渐向后喷气,并设运载物所获得的速度依次为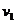 、
、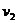 和
和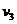 ,则由动量守恒定律得
,则由动量守恒定律得
第一级火箭喷完后
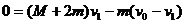
第二级火箭喷完后
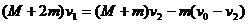
第三级火箭喷完后
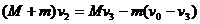
解上面的三式,得
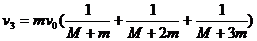
而 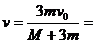
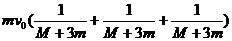
显然 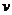 <
<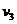
所以,火箭不是一次把燃气喷完,而是逐渐向后喷气以获得更大反冲速度的道理就在这里。
命题解读:此题的难点在于题目中所给的发射火箭时喷出的气体速度都是相对于火箭的,运用动量守恒定律列式求解时,一定要把这个速度转化成为相对于地面的速度;逐级发射火箭时,每一次发射都有与之相对应的动量守恒定律方程,并且每次发射时火箭的速度和质量都是不同的,列式是一定不要出错。
2.动量守恒定律
⑴动量是否守恒的判断
例题8.把一支枪水平固定在小车上,小车放在光滑的水平地面上,枪发射出子弹时,关于枪、子弹和小车的下列说法中正确的是
 .枪和子弹组成的系统动量守恒
.枪和子弹组成的系统动量守恒
 .枪和小车组成的系统动量守恒
.枪和小车组成的系统动量守恒
 .只有在忽略子弹和枪筒之间的摩擦的情况下,枪、子弹和小车组成的系统动量才近似守恒
.只有在忽略子弹和枪筒之间的摩擦的情况下,枪、子弹和小车组成的系统动量才近似守恒
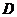 .枪、子弹和小车组成的系统动量守恒
.枪、子弹和小车组成的系统动量守恒
解析:对于枪和子弹自成的系统,在发射子弹时由于枪水平方向上受到小车对它的作用力,所以动量是不守恒的,选项 错;同理,对于枪和小车所组成的系统,在发射子弹的瞬间,枪受到火药对它的推力作用,因此动量也是不守恒的,选项
错;同理,对于枪和小车所组成的系统,在发射子弹的瞬间,枪受到火药对它的推力作用,因此动量也是不守恒的,选项 错;对于枪、子弹和小车组成的系统而言,火药爆炸产生的推力以及子弹和枪筒之间的摩擦力都是系统的内力,没有外力作用在系统上,所以这三者组成的系统动量是守恒的,选项
错;对于枪、子弹和小车组成的系统而言,火药爆炸产生的推力以及子弹和枪筒之间的摩擦力都是系统的内力,没有外力作用在系统上,所以这三者组成的系统动量是守恒的,选项 错,
错,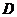 正确。
正确。
故,答案选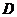 。
。
命题解读:判断动量是否守恒,首先要看清系统是由哪些物体所组成的,然后再根据动量守恒的条件进行判断(具备下列条件之一即可):
①系统不受外力;
②系统受外力,但外力的合力为零;
③系统在某一方向上不受外力或合外力为零;
④系统所受的外力远小于内力或某一方向上外力远小于内力。
满足前三条中的任何一个条件,系统的动量都是守恒的,满足第四个条件时系统的动量是近似守恒。动量守恒是自然界普遍适用的基本规律之一,它既适用于宏观、低速的物体,也适用于微观、高速的物体。
⑵系统和过程的选取----动量守恒定律的一般应用
例题9.两只小船相向航行,速度大小均为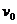 ,每只船(连同船上的人、物)的质量均为
,每只船(连同船上的人、物)的质量均为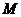 。当它们“擦肩”而过时,各把质量为
。当它们“擦肩”而过时,各把质量为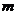 的物体从船侧同时投放到对方船上去,则船的速度大小变为多大?(忽略水的阻力)
的物体从船侧同时投放到对方船上去,则船的速度大小变为多大?(忽略水的阻力)
解析:先选投出的物体和剩余部分为第一个系统,并设每只船将质量为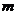 的物体从船侧头出后,剩余部分的速度大小为
的物体从船侧头出后,剩余部分的速度大小为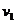 ,船的运动方向为正方向,则由动量守恒定律得
,船的运动方向为正方向,则由动量守恒定律得
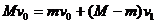
再选这剩余的部分和对方船上投过来的质量为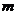 的物体作为第二个系统,设两者的共同速度为
的物体作为第二个系统,设两者的共同速度为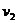 ,则由动量守恒定律得
,则由动量守恒定律得
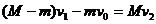
解以上两式得
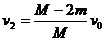
故,两船最后的速度大小都变为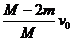 。
。
命题解读:利用动量守恒定律解题首先需要解决下面的两个问题:
一是要解决相互作用的过程,确定初、末状态。上面的题目非常典型,因里面涉及的物体多、过程复杂,分析和解决问题时一般都是按阶段、分步骤来进行,解决的关键是要认真、仔细地分析相互作用的过程,合理、清晰地确定研究对象----系统。
二是要设出正方向。因为动量守恒定律的表达式是个矢量式,只有规定好了正方向后,才能确定每个矢量的正、负,从而将已知量带入进行求解。
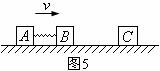 对应训练.如图5所示,用轻弹簧相连的质量均为
对应训练.如图5所示,用轻弹簧相连的质量均为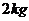 的
的 、
、 两物块均以
两物块均以 的速度在光滑水平地面上运动,弹簧处于原长,另一质量为
的速度在光滑水平地面上运动,弹簧处于原长,另一质量为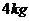 的物块
的物块 静止在前方。
静止在前方。 与
与 碰撞后二者粘在一起运动。试求在以后的运动中,当弹簧的弹性势能最大时,物块
碰撞后二者粘在一起运动。试求在以后的运动中,当弹簧的弹性势能最大时,物块 的速度多大?最大的弹性势能是多少?
的速度多大?最大的弹性势能是多少?
解析:物块 与
与 先发生相互作用,其作用的时间极短,设作用后的共同速度为
先发生相互作用,其作用的时间极短,设作用后的共同速度为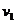 ,则由动量定理得
,则由动量定理得
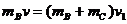
所以 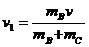
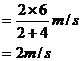
之后,物块 通过弹簧与刚达到共同速度的
通过弹簧与刚达到共同速度的 、
、 这个小整体发生相互作用,弹簧从此被压缩,弹簧产生的弹力使物块
这个小整体发生相互作用,弹簧从此被压缩,弹簧产生的弹力使物块 减速,使
减速,使 、
、 这个小整体加速,并且只要物块
这个小整体加速,并且只要物块 的速度大于
的速度大于 、
、 这个小整体的速度,弹簧就继续被压缩,直到
这个小整体的速度,弹簧就继续被压缩,直到 、
、 、
、 三者达到共同速度,弹簧的压缩量才达到最大,即系统的弹性势能此时达到最大值。设
三者达到共同速度,弹簧的压缩量才达到最大,即系统的弹性势能此时达到最大值。设 、
、 、
、 三者达到共同速度为
三者达到共同速度为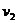 ,则对于这三者组成的系统来说,由动量守恒定律得
,则对于这三者组成的系统来说,由动量守恒定律得
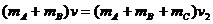
所以 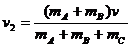
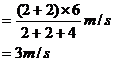
此即为弹簧的弹性势能最大时物块 的速度大小,弹性势能的最大值为
的速度大小,弹性势能的最大值为

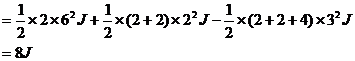
命题解读:此题的难点有二:一是通过作用过程的分析,得出 、
、 、
、 三者达到共同速度时,弹簧的压缩量达到最大,此时系统的弹性势能达到最大值;二则是在求解最大弹性势能时,很可能会出现
三者达到共同速度时,弹簧的压缩量达到最大,此时系统的弹性势能达到最大值;二则是在求解最大弹性势能时,很可能会出现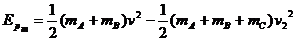 这样的的运算,显然这个表达式是错误的,它是不满足能量守恒定律的,原因是在物块
这样的的运算,显然这个表达式是错误的,它是不满足能量守恒定律的,原因是在物块 与
与 发生相互作用的过程中已经损失了一部分能量。
发生相互作用的过程中已经损失了一部分能量。
⑶系统的总动量不守恒,但在某一方向上动量守恒
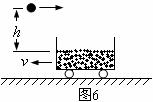 例题10.如图6所示,将质量
例题10.如图6所示,将质量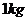 的铅球一水平向右的初速度
的铅球一水平向右的初速度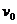 抛出,落入一个质量
抛出,落入一个质量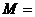
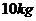 、以水平速度
、以水平速度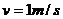 向左运动的装着砂子的小车中,小车与水平面的摩擦不计。已知铅球刚被抛出时离车内砂面的竖直高度
向左运动的装着砂子的小车中,小车与水平面的摩擦不计。已知铅球刚被抛出时离车内砂面的竖直高度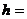
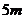 ,为使小车被铅球撞击后不再继续向前运动,则
,为使小车被铅球撞击后不再继续向前运动,则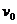 至少多大?
至少多大?
解析:铅球落入砂车时,由于碰撞,铅球与砂车促成的系统,在竖直方向上支持力大于重力,而水平方向上不受外力作用,故系统的总动量不守恒,但在水平方向上的分动量是守恒的。
设铅球的质量为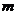 ,铅球落入砂车后的共同速度为
,铅球落入砂车后的共同速度为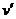 ,并取水平向右为正方向,依题意,刹车不能继续前进的条件为
,并取水平向右为正方向,依题意,刹车不能继续前进的条件为
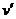 ≥
≥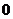
因铅球做平抛运动,其水平方向上的速度不变,则对于铅球和砂车组成的系统,在水平方向上由动量定理得
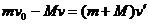
联立以上两式,得
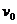 ≥
≥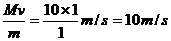
即,铅球被抛出时的最小初速度为 。
。
命题解读:系统所受的合外力不为零,则其动量是不守恒的,但如果在某一方向上满足动量守恒的条件,则在这一方向上动量是守恒的。类似的情况还要不少,例如,在地面阻力可忽略不计的情况下,大炮斜发炮弹;在水的阻力不计的情况下,站在船头的人斜向上跳起等等。
⑷内力远大于外力,动量近似守恒的问题
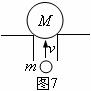 例题11.如图7所示,质量为
例题11.如图7所示,质量为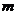 的子弹以速度
的子弹以速度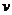 从正下方向上击穿一个质量为
从正下方向上击穿一个质量为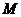 木球。若击穿后木球上升的最大高度为
木球。若击穿后木球上升的最大高度为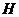 ,求击穿木球后子弹最多能上升多高?
,求击穿木球后子弹最多能上升多高?
解析:子弹在击穿木球时属于打击问题,子弹和木球之间的作用力远大于两者的重力和支持力的合力,故可认为在竖直方向上,子弹和木球组成的系统动量近似守恒。又因为作用时间很短,所以可认为木球在这段时间内尚未发生位移但获得了速度,子弹穿透木球后,子弹和木球分别做竖直上抛运动。
设子弹穿透木球后,子弹和木球的速度分别为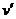 和
和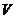 ,竖直方向上由动量定理可得
,竖直方向上由动量定理可得
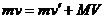
设子弹做竖直上抛运动的最大高度为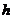 ,对于子弹和木球,由运动学知识分别可得
,对于子弹和木球,由运动学知识分别可得
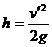 ,
,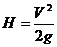
联立以上三式,得

命题解读:解决本题要抓住两点,一是子弹和木球作用过程中内力远大于外力,竖直方向上动量近似守恒;二是由于子弹和木球的作用时间很短,子弹穿出木球的瞬间,可认为木球的位置未动就会得了速度。再如,炸弹在空中沿竖直方向炸裂,也属于内力远大于外力的情况。
⑸人、船模型中的位移求解----平均动量守恒问题
 例题12.一质量为
例题12.一质量为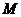 、底边长为
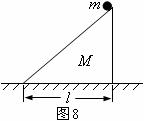
、底边长为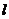 的三角形斜劈静止于光滑的水平桌面上,如图8所示。有一质量为
的三角形斜劈静止于光滑的水平桌面上,如图8所示。有一质量为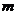 的小球由斜劈的顶部无初速滑到底部,试求斜劈发生的位移为多大?
的小球由斜劈的顶部无初速滑到底部,试求斜劈发生的位移为多大?
解析:小球和斜劈组成的系统在整个的运动过程中都不受水平方向的外力作用,所以水平方向上系统的平均动量守恒。
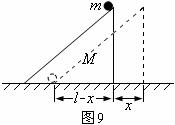 设在小球由斜劈顶部滑到底部的过程中,斜劈发生的位移大小为
设在小球由斜劈顶部滑到底部的过程中,斜劈发生的位移大小为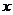 ,画出示意图如图9所示,并规定斜劈的运动方向为正,则由动量守恒定律得
,画出示意图如图9所示,并规定斜劈的运动方向为正,则由动量守恒定律得
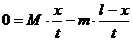
解得 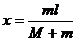
命题解读:①小球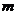 和斜劈
和斜劈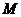 所组成的系统水平方向上是平均动量守恒,这是对全过程来说的,其实任意时刻水平方向上的总动量等于零。
所组成的系统水平方向上是平均动量守恒,这是对全过程来说的,其实任意时刻水平方向上的总动量等于零。
②对这样的人、船模型,如果设全过程中两者对地位移大小分别为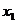 和
和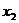 ,则根据上题中的分析结果,可得到下面的等式
,则根据上题中的分析结果,可得到下面的等式
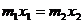
这样,就把原来动量守恒定律表达式中物体质量与速度的关系转化成了物体质量与对地位移的关系,求解位移时就可以直接利用这个结论。但要注意这个表达式适用的条件是相互作用的这两个物体原来都静止。
(6)拖车脱钩中的位移巧解
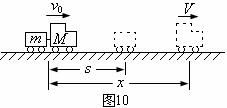 例题13.如图10所示,质量为
例题13.如图10所示,质量为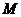 的卡车牵引一质量为
的卡车牵引一质量为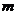 的拖车在水平路面上以速度
的拖车在水平路面上以速度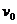 匀速行驶,某一时刻拖车脱钩,由于当时司机没有发觉,所以卡车继续前进,拖车滑行距离
匀速行驶,某一时刻拖车脱钩,由于当时司机没有发觉,所以卡车继续前进,拖车滑行距离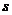 而停止,试求从拖车脱钩到停止的这一过程中,卡车行驶的距离多大?
而停止,试求从拖车脱钩到停止的这一过程中,卡车行驶的距离多大?
解析:把卡车和拖车看作一个系统,因脱钩前系统匀速运动,所以动量是守恒的。规定运动方向为正方向,并设拖车停止时卡车的运动速度为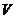 ,如图10所示,则
,如图10所示,则
(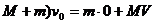
又因为拖车脱钩后,两部分都作匀变速运动,若设从拖车脱钩到停止的这一过程中,卡车行驶的距离为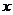 ,则
,则
对于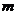
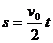
对于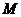
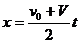
解以上三式,得
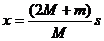
命题解读:本题解决的技巧在于根据系统的动量守恒列式求出拖车停止时卡车的速度。
⑺动量守恒定律的相对性
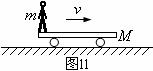 例题14.质量为
例题14.质量为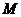 的小车尾部站有一质量为
的小车尾部站有一质量为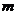 的人,人和小车以共同的速度
的人,人和小车以共同的速度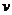 在光滑的水平面上向前行驶,如图11所示。当人相对于小车以水平速度
在光滑的水平面上向前行驶,如图11所示。当人相对于小车以水平速度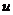 向后跳出时,小车的速度为多少?
向后跳出时,小车的速度为多少?
解析:人在小车上跳起的瞬间,人和小车组成的系统在水平方向上不受外力作用,所示满足动量守恒的条件。
以人和小车原来的运动方向为正方向,设人跳出时车的速度变为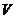 ,则人跳出时相对于地面的速度为(
,则人跳出时相对于地面的速度为(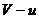 ),则由动量守恒定律得
),则由动量守恒定律得
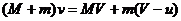
解得 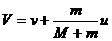
命题解读:动量守恒定律表达式中中各动量均是相对于同一参考系的,否则,就要选择同一参考系进行转换。注意在进行转换时一定要根据选取的正方向,判断准各动量的正、负,方向不明确的一般以正方向代入,如上题中的人跳出小车后的对地速度。
⑻隐含条件的分析
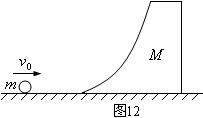 例题15.光滑的水平面上静置一质量为
例题15.光滑的水平面上静置一质量为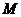 的带有光滑圆弧轨道的滑块,如图12所示。另有一质量为
的带有光滑圆弧轨道的滑块,如图12所示。另有一质量为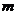 的小球以水平速度
的小球以水平速度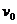 沿水平面冲上滑块,,设滑块足够高,试求小球所能达到的最大高度。
沿水平面冲上滑块,,设滑块足够高,试求小球所能达到的最大高度。
解析:小球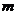 在滑块上达到最大高度时,它和滑块达到共同速度。对这两者组成的系统,水平方向上动量守恒,设它们的共同速度为
在滑块上达到最大高度时,它和滑块达到共同速度。对这两者组成的系统,水平方向上动量守恒,设它们的共同速度为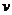 ,则
,则
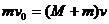
两者组成的系统能量也是守恒的,设小球沿滑块上升的最大高度为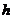 ,则
,则
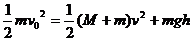
解以上两式得
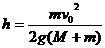
命题解读:小球沿滑块上升到最大高度,意味着它相对于滑块没有竖直和水平方向上的速度,即相对于滑块已经静止,这就是这个题目中隐含的条件。所以在分析问题时,不仅要利用好题中所给的现有的已知量,还要从题目的叙述中挖掘出隐含的条件,从而顺利解题。
 对应训练:在光滑的水平轨道上有两个半径都是
对应训练:在光滑的水平轨道上有两个半径都是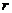 的小球
的小球 和
和 ,质量分别是
,质量分别是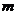 和
和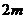 ,当两球心之间的距离大于
,当两球心之间的距离大于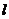 (
(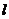 ≫
≫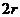 )时,两球无相互作用力,而当两球心之间的距离小于或等于
)时,两球无相互作用力,而当两球心之间的距离小于或等于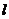 时,两球存在着恒定的斥力
时,两球存在着恒定的斥力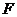 。设小球
。设小球 从远离
从远离 球处以速率
球处以速率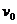 沿两球连心线向原来静止的
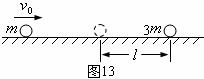
沿两球连心线向原来静止的 球运动(如图13所示)。欲使两球不发生碰撞,
球运动(如图13所示)。欲使两球不发生碰撞,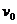 必须满足什么条件?
必须满足什么条件?
解析:依题意,为了避免两球发生碰撞,应该是两者刚要接触时就达到共同速度。
设小球 的最大初速度为
的最大初速度为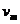 ,两者的共同速度为
,两者的共同速度为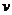 ,则由动量守恒定律得
,则由动量守恒定律得

从 和
和 发生相互作用到两者达到共同速度的整个过程中,由能量守恒定律得
发生相互作用到两者达到共同速度的整个过程中,由能量守恒定律得
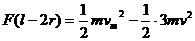
解得 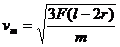
所以,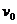 必须满足的条件是
必须满足的条件是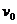 ≤
≤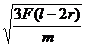 。
。
命题解读:此题除了要注意隐含条件的分析以外,还要明确两个小球能够靠近的最小距离是两个小球的半径之和,否则,在列第二个方程时会错列成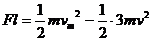 导致结果错误。
导致结果错误。
⑼动量守恒与能量
例题16.如图14所示,两块带有等量异号电荷的平行金属板分别固定在长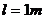 的绝缘板的两端,组成一带电框架,框架右端带负电的金属板上固定一根原长为
的绝缘板的两端,组成一带电框架,框架右端带负电的金属板上固定一根原长为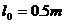 绝缘轻弹簧,框架的总质量
绝缘轻弹簧,框架的总质量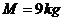 。由于带电,两金属板间产生了
。由于带电,两金属板间产生了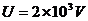 的高压。现有一质量
的高压。现有一质量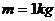 、带电
、带电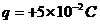 的带电小球(可看作质点,且不影响金属板间的匀强电场)将弹簧压缩
的带电小球(可看作质点,且不影响金属板间的匀强电场)将弹簧压缩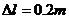 后用线拴住,,因而弹簧具有了
后用线拴住,,因而弹簧具有了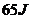 的弹性势能。现使整个装置在光滑水平面上以
的弹性势能。现使整个装置在光滑水平面上以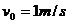 的速度向右运动,运动过程中拴小球的细线突然断裂,从而小球被弹开,不计一切摩擦,且电势能的变化量等于电场力和相对于电场方向的位移的乘积。试求
的速度向右运动,运动过程中拴小球的细线突然断裂,从而小球被弹开,不计一切摩擦,且电势能的变化量等于电场力和相对于电场方向的位移的乘积。试求
 ⑴当小球刚好被弹簧弹开时,小球与框架的速度分别为多大?
⑴当小球刚好被弹簧弹开时,小球与框架的速度分别为多大?
⑵通过分析计算回答:在细线断裂后的运动中,小球能否与左端的金属板发生接触?
解析:⑴当弹簧刚恢复到原长时小球和弹簧分离,设此时小球和框架的速度分别为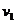 和
和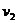 ,根据动量守恒和能量守恒定律分别有
,根据动量守恒和能量守恒定律分别有
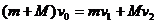
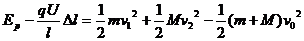
解得 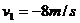 ,
,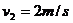
⑵当小球与框架的速度相等时,小球相对于框架的位移最大,此时两者达到共同速度,根据动量守恒,此共同速度仍为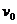 。设从小球被弹开到两者达到共同速度
。设从小球被弹开到两者达到共同速度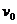 小球和框架对地位移分别为
小球和框架对地位移分别为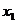 和
和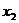 ,则由动能定理得
,则由动能定理得
对小球 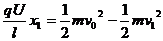
对框架 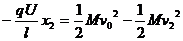 ,
,
解得 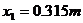 ,
,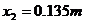
显然 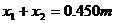 <
<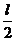 ,小球不会碰到左侧的金属板。
,小球不会碰到左侧的金属板。
命题解读:动量守恒定律的应用多年来一直是高考的重点、热点和难点,此类题目较少是单纯的动量守恒问题,常常伴随着能量守恒,有时又与物理学的其她知识相联系,如电场、磁场等等。本题是一道与电场相联系的题目,是一道背景源于电场而本质上又是动量守恒定律应用的典型题目。
1.动量定理
⑴易混淆的概念
例题1.下列说法中正确的是
①动量大的物体惯性一定大
②动量大的物体运动一定快
③动量相同的物体运动方向一定相同
④动量等于物体所受合外力的冲量
⑤物体所受合外力的冲量就是动量的增量
⑥物体所受合外力的冲量等于动量的增量
 .①④⑥
.①④⑥
 .③⑥
.③⑥
 .①③⑥
.①③⑥
 .②⑤
.②⑤
解析:物体的质量和运动速度的乘积(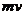 )叫做动量,可见动量的大小与两个因素有关系,动量大质量不一定大,即惯性不一定大,运动也不一定就快,所以①、②都是错误的;动量是一个矢量,它的方向与速度的方向一定相同,所以③是正确的;根据动量定理的表达式
)叫做动量,可见动量的大小与两个因素有关系,动量大质量不一定大,即惯性不一定大,运动也不一定就快,所以①、②都是错误的;动量是一个矢量,它的方向与速度的方向一定相同,所以③是正确的;根据动量定理的表达式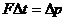 中,等号的左边是物体所受合外力的冲量,而右边则是时间
中,等号的左边是物体所受合外力的冲量,而右边则是时间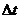 内物体动量的增量,它们是不同的物理量,只是数值相等,所以用“=”连接,但绝不能说“物体所受合外力的冲量就是动量的增量”,更不能说“动量等于物体所受合外力的冲量”,所以④、⑤都是错误的,只有⑥是正确的。
内物体动量的增量,它们是不同的物理量,只是数值相等,所以用“=”连接,但绝不能说“物体所受合外力的冲量就是动量的增量”,更不能说“动量等于物体所受合外力的冲量”,所以④、⑤都是错误的,只有⑥是正确的。
故,本题答案选 。
。
命题解读:此题考查了动量、冲量的概念,以及物体所受合外力冲量与物体动量变化的关系,即动量定理。动量和冲量虽然单位“等效”,但它们是不同的物理量,动量表示物体运动量的大小,即描述的是物体在某一时刻的运动效果,是一个状态量;而冲量则是力对时间的积累效果,对应于一段时间,冲量是一个过程量。至于动量定理,它解决了物体所受所有外力的合力对物体的冲量与此过程中物体总的动量变化之间的关系,尽管它们都是矢量,并且方向也相同,但一定要注意的是等号左右两边是两个不同的物理量,之所以用“=”连接,只是数值相等,仅此而已!
⑵动量定理的一般应用----解题的基本方法
例题2.蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做出各种空中动作的运动项目。一个质量为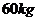 的运动员,从离水平网面
的运动员,从离水平网面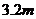 高处自由落下,着网后又沿竖直方向蹦回离水平网面
高处自由落下,着网后又沿竖直方向蹦回离水平网面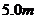 高处。已知运动员与网接触的时间为
高处。已知运动员与网接触的时间为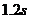 ,若把这段时间内网对运动员的作用力当作恒力来处理,求此力的大小。
,若把这段时间内网对运动员的作用力当作恒力来处理,求此力的大小。
解析(一):运动员刚接触网时的速度大小为
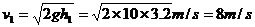 ,方向向下。
,方向向下。
刚离开网时的速度大小为
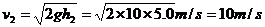 ,方向向上。
,方向向上。
运动员与网接触的过程中,设网对运动员的作用力大小为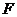 ,并设向上为正方向,对运动员由动量定理,则有
,并设向上为正方向,对运动员由动量定理,则有
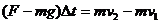
则 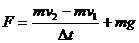

解析(二):以运动员下降、与网接触、上升三个阶段全程考虑。
从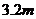 高处自由下落的时间为
高处自由下落的时间为
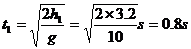
从反弹到弹回到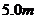 高处所用的时间为
高处所用的时间为
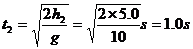
整个过程中运动员始终受重力作用,仅在与网接触的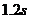 内受到网对他向上的弹力
内受到网对他向上的弹力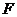 作用,若设竖直向上为正方向,则全程利用动能定理得
作用,若设竖直向上为正方向,则全程利用动能定理得
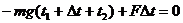
所以 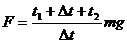
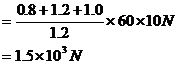
命题解读:①动量定理的表达式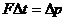 是个矢量式,解题时一定要设出正方向,题中已知的矢量中,与所设正方向相同的代入正值,反之代入负值,对于方向未知的矢量,先认为与所设的正方向相同,求出的值为正就表示它确实就是沿正方向的,否则与所设的正方向相反。
是个矢量式,解题时一定要设出正方向,题中已知的矢量中,与所设正方向相同的代入正值,反之代入负值,对于方向未知的矢量,先认为与所设的正方向相同,求出的值为正就表示它确实就是沿正方向的,否则与所设的正方向相反。
②动量定理的表达式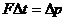 中的
中的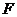 应是物体所受的合外力,但作用在物体上的力,并非作用时间都是相同的,这时可以分阶段利用定理进行列式求解,也可以全过程列式求解象上面的解析(二)。全程列式时,一定要注意每一个力作用的时间阶段。
应是物体所受的合外力,但作用在物体上的力,并非作用时间都是相同的,这时可以分阶段利用定理进行列式求解,也可以全过程列式求解象上面的解析(二)。全程列式时,一定要注意每一个力作用的时间阶段。
③现在可以回忆一下前面所学习的动能定理的应用,当时涉及的物理量有力、初速度、末速度,另外还有物体发生的位移,和现在的动量定理的应用比较就可以看出,唯一不同的就是把位移换成了时间。所以,过程涉及位移时考虑用动能定理,而涉及时间时考虑用动量定理。
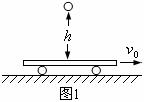 对应训练:如图1所示,质量为
对应训练:如图1所示,质量为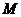 的小车在光滑的水平面上以速度
的小车在光滑的水平面上以速度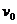 向右做匀速直线运动,一个质量为
向右做匀速直线运动,一个质量为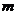 的小球从高
的小球从高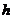 处自由下落,与小车碰撞后反弹上升的高度为仍为
处自由下落,与小车碰撞后反弹上升的高度为仍为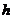 。设
。设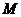 ≫
≫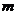 ,发生碰撞时弹力
,发生碰撞时弹力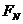 ≫
≫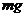 ,小球与车之间的动摩擦因数为
,小球与车之间的动摩擦因数为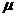 ,则小球弹起时的水平速度可能是
,则小球弹起时的水平速度可能是
 .
.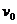
 .
.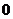
 .
.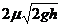
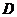 .
.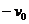
解析:小球的水平速度是由于小车对它的摩擦力作用引起的,若小球在离开小车之前水平方向上就已经达到了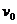 ,则摩擦力消失,小球在水平方向上的速度不再加速;反之,小球在离开小车之前在水平方向上就是一直被加速的。故分以下两种情况进行分析:
,则摩擦力消失,小球在水平方向上的速度不再加速;反之,小球在离开小车之前在水平方向上就是一直被加速的。故分以下两种情况进行分析:
小球离开小车之前已经与小车达到共同速度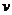 ,则水平方向上动量守恒,有
,则水平方向上动量守恒,有
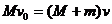
由于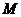 ≫
≫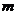
所以 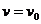
若小球离开小车之前始终未与小车达到共同速度,则对小球应用动量定理得
水平方向上有
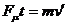
竖直方向上有
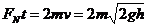
又 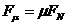
解以上三式,得
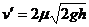
故,正确的选项为
 。
。
误点警示:此题的特点是对小球要从竖直和水平两个方向上利用动量定理进行讨论,但在分析的过程中,可能会出现漏选的情况,即没有考虑到小球和小车有达到共同速度的可能。在平常做题的过程中,要严谨、细心、周密,培养出良好的学习习惯。
⑶动量定理巧应用之一----对生活中一些现象的解释
例题3.玻璃杯同一高度下落下,掉在水泥地上比掉在草地上容易碎,这是由于玻璃杯与水泥地撞击的过程中
 .玻璃杯的动量较大
.玻璃杯的动量较大
 .玻璃杯受到的冲量较大
.玻璃杯受到的冲量较大
 .玻璃杯的动量变化较大
.玻璃杯的动量变化较大
 .玻璃杯的动量变化较快
.玻璃杯的动量变化较快
解析:玻璃杯从相同的高度落下,落地时的速度大小是相同的,经过与地面撞击,最后速度都变为零,所以无论是落在水泥地上还是落在草地上,玻璃杯动量的变化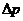 是相同的,由动量定理
是相同的,由动量定理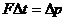 可知,两种情况下玻璃杯受到的合外力的冲量也是相同的,所以选项
可知,两种情况下玻璃杯受到的合外力的冲量也是相同的,所以选项 、
、 和
和 都是错误的;但由于掉在水泥地上时,作用的时间
都是错误的;但由于掉在水泥地上时,作用的时间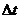 较短,所以玻璃杯受到的合外力的冲力较大,若把动量定理的表达式写成
较短,所以玻璃杯受到的合外力的冲力较大,若把动量定理的表达式写成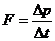 ,就可以得出玻璃杯易碎的原因是“玻璃杯的动量变化较快”,所以选项
,就可以得出玻璃杯易碎的原因是“玻璃杯的动量变化较快”,所以选项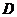 是正确的。
是正确的。
命题解读:本题利用动量定理解释了一个生活中很常见的例子,解决问题的关键在于抓住了两种情况中“动量变化相等”,而“作用时间不等”这两个特点。类似的现象还有很多,如跳高时落在海绵垫上,跳远时落在沙坑里,船靠码头时靠在车胎上,电器包装在泡沫塑料垫上,人从高处跳下时先用脚尖着地等等,道理都是如此。
⑷动量定理巧用之二----求变力的冲量
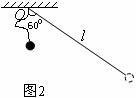 例题4.如图2所示,长为
例题4.如图2所示,长为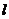 的轻绳的一端固定在
的轻绳的一端固定在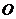 点,另一端系一质量为
点,另一端系一质量为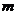 的小球,将小球从
的小球,将小球从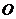 点正下方
点正下方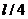 处以一定的初速度水平向右抛出,经一定时间的运动轻绳被拉直,以后小球将以
处以一定的初速度水平向右抛出,经一定时间的运动轻绳被拉直,以后小球将以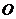 点为圆心在竖直平面内摆动。已知轻绳刚被拉直时绳与竖直方向成
点为圆心在竖直平面内摆动。已知轻绳刚被拉直时绳与竖直方向成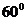 角,试求
角,试求
⑴小球被水平抛出时的初速度;
⑵在轻绳被拉直的瞬间,圆心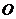 点受到的冲量。
点受到的冲量。
解析:⑴设经过时间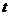 轻绳被拉直,则由平抛运动的规律可得
轻绳被拉直,则由平抛运动的规律可得
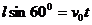
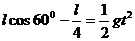
解以上两式,得
 ,
,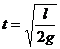
⑵轻绳刚被拉直的瞬间,小球的瞬时速度为
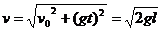
设速度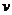 与竖直方向的夹角为
与竖直方向的夹角为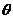 ,则
,则

所以 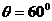
显然,这与轻绳和竖直方向的夹角是相同的,则小球该时刻的动量为
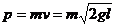
设轻绳被拉直的方向为正方向,则由动量定理得
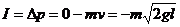
故,圆心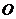 点受到的冲量大小为
点受到的冲量大小为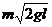 ,方向沿轻绳斜向下。
,方向沿轻绳斜向下。
命题解读:本题涉及了平抛运动和动量定理两部分的知识,特别是第⑵问求解圆心 点受到的冲量大小时,由于轻绳张力是变力,况且大小也不知道,无法用
点受到的冲量大小时,由于轻绳张力是变力,况且大小也不知道,无法用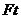 直接求解,所以根据动量定理用物体动量的变化量等效代替变力的冲量是非常方便的。
直接求解,所以根据动量定理用物体动量的变化量等效代替变力的冲量是非常方便的。
⑸动量定理巧用之三----巧解曲线运动中的动量变化
例题5.将一质量为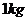 的物体以速度
的物体以速度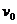 抛出,若在抛出后
抛出,若在抛出后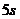 钟落地,不计空气阻力,试求此物体在落地前
钟落地,不计空气阻力,试求此物体在落地前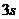 内的动量变化。
内的动量变化。
解析:物体被抛出后仅受重力作用,所以由动量定理得
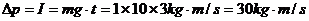
故,物体落地前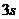 内的动量变化为
内的动量变化为 ,方向竖直向下。
,方向竖直向下。
命题解读:该题中的物体被抛出后,做一般的曲线运动,如果想直接求出它在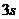 内的动量变化是不可能的。但由于物体所受的外力只有重力,所以利用动量定理求出合外力的冲量巧妙地等效代替物体动量的变化。从这个例子看出,只要物体所受的合外力是个恒力,根据动量定理就可以求出任意一段时间内物体动量的变化。
内的动量变化是不可能的。但由于物体所受的外力只有重力,所以利用动量定理求出合外力的冲量巧妙地等效代替物体动量的变化。从这个例子看出,只要物体所受的合外力是个恒力,根据动量定理就可以求出任意一段时间内物体动量的变化。
(6)动量定理巧用之四----“流体”类问题中动量定理的运用
例题6.一艘帆船在静水中由于风力的推动而做匀速直线运动,帆面的面积为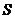 ,风速为
,风速为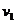 ,船速为
,船速为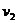 (
(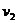 <
<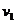 ),空气密度为
),空气密度为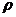 ,帆船在匀速前进的过程中帆面所受到的平均风力大小为多少?
,帆船在匀速前进的过程中帆面所受到的平均风力大小为多少?
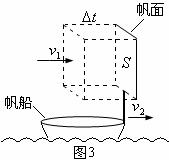 解析:依题意画出示意图如图3所示,以帆船为参考系,从帆面开始逆着风的方向取长度为
解析:依题意画出示意图如图3所示,以帆船为参考系,从帆面开始逆着风的方向取长度为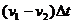 的一段空气柱为研究对象,这部分空气的质量为
的一段空气柱为研究对象,这部分空气的质量为
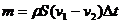
这部分空气经过时间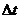 后,相对于帆面速度都变为
后,相对于帆面速度都变为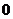 ,设帆船前进的方向为正方向,对这部分空气柱则由动量定理得
,设帆船前进的方向为正方向,对这部分空气柱则由动量定理得
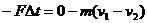
式中的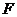 为帆面对空气柱的平均作用力大小,由牛顿第三定律可知,帆面所受到的平均风力大小为
为帆面对空气柱的平均作用力大小,由牛顿第三定律可知,帆面所受到的平均风力大小为
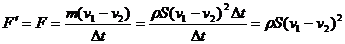
命题解读:对于象气体、液体这种没有形状和大小的流体而言,解决的方法就是根据题意取出与一段时间相对应的一定长度的这种物体,即,想办法“找出”形状和大小,求出其质量,然后根据其动量变化,利用动量定理列出方程进行求解。
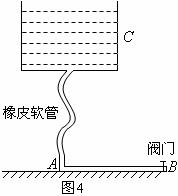 对应训练:如图4所示,置于高处的大水槽
对应训练:如图4所示,置于高处的大水槽 ,通过一根竖直的橡皮软管与置于水平面上的长直钢管的
,通过一根竖直的橡皮软管与置于水平面上的长直钢管的 端连接,软管与
端连接,软管与 连接处互相垂直,水平钢管的末端
连接处互相垂直,水平钢管的末端 处有一阀门。现在把阀门打开,水槽中的水正在流出,水流在水平钢管中的流速
处有一阀门。现在把阀门打开,水槽中的水正在流出,水流在水平钢管中的流速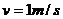 ,当迅速地把阀门关闭(历时
,当迅速地把阀门关闭(历时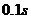 )时,试求管内水柱对阀门的平均冲击力。已知钢管长
)时,试求管内水柱对阀门的平均冲击力。已知钢管长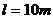 ,其内径
,其内径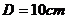 ,水的密度
,水的密度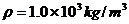 ,忽略水与管壁的摩擦。
,忽略水与管壁的摩擦。
解析:由于橡皮软管与钢管在 处的连接是相互垂直的,因此,对阀门形成冲击的是水平钢管中
处的连接是相互垂直的,因此,对阀门形成冲击的是水平钢管中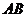 段的水柱。以
段的水柱。以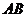 段的水柱为研究对象,它的质量为
段的水柱为研究对象,它的质量为
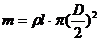
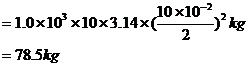
设水流方向为正方向,由动量定理得
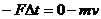
式中的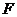 为阀门对水柱的平均作用力,由牛顿第三定律可知水柱对阀门的平均冲击力大小为
为阀门对水柱的平均作用力,由牛顿第三定律可知水柱对阀门的平均冲击力大小为
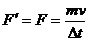
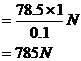
即,水流对阀门的平均冲力的大小为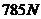 ,方向与水流方向相同。
,方向与水流方向相同。
命题解读:此题与上面的例题不同的地方是没有在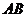 段上任意地取一段水柱,而是取了
段上任意地取一段水柱,而是取了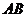 段上的全部水柱,原因是在极短的时间
段上的全部水柱,原因是在极短的时间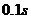 内,这部分水柱的动量都由原来的
内,这部分水柱的动量都由原来的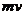 减小到零。
减小到零。
⑺动量定理巧用之五----系统中动量定理的应用
例题7.总质量为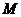 的列车沿平直轨道匀速行驶,其末节车厢质量为
的列车沿平直轨道匀速行驶,其末节车厢质量为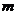 ,中途脱钩,司机发觉时列车已行驶了时间
,中途脱钩,司机发觉时列车已行驶了时间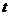 ,于是司机立即关闭油门,列车滑行前进。设车运动阻力与车重成正比,机车的牵引力不变,当列车和车厢都静止时,求列车比车厢多行驶的时间
,于是司机立即关闭油门,列车滑行前进。设车运动阻力与车重成正比,机车的牵引力不变,当列车和车厢都静止时,求列车比车厢多行驶的时间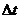 。
。
解析:列车比车厢多行驶时间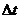 ,就要多克服阻力对它的冲量
,就要多克服阻力对它的冲量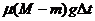 ,列车多克服的冲量是由列车多出的动量
,列车多克服的冲量是由列车多出的动量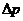 提供的,而列车多次出的动量
提供的,而列车多次出的动量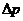 又是由列车的牵引力在时间
又是由列车的牵引力在时间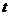 内对列车产生的冲量
内对列车产生的冲量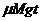 造成的,于是有
造成的,于是有
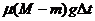
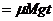
所以 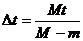
命题解读:此题如果采用常规解法,即分别以列车和车厢为研究对象,对每一个研究对象都按其运动过程利用动量定理列式求解,可能要列出好多的方程,一是麻烦,再者也没有什么新意。上面的解法,把两者作为一个系统来考虑,只列出一个方程就顺利地解决了问题,思路清晰,说理深刻,解法简洁明快,具有创新意识,使问题的解决大大简化。
2.分散系的比较
|
分散系 种类 |
溶液 |
胶体 |
浊液 |
|||
|
水溶液 |
非水溶液 |
粒子胶体 |
分子胶体 |
悬浊液 |
乳浊液 |
|
|
分散质粒子 |
离子或分子 |
分子 |
分子或离子的集合体 |
大分子 |
巨量分子集合的颗粒 |
巨量分子集合的液滴 |
|
举例 |
食盐水 |
碘酒 |
Fe(OH)3胶体 |
淀粉溶液 |
石灰乳 |
牛奶 |
|
分散质粒子直径⑴ |
1n m |
1nm-100n m |
100n m |
|||
|
均一性⑵ |
|
|
|
|||
|
稳定性⑶ |
|
|
久置沉降 |
久置分层 |
||
|
能否通过滤纸⑷ |
|
|
|
|||
|
能否通过半透膜⑸ |
|
|
|
|||
|
有无丁达尔效应⑹ |
|
|
- |
试题枚举
[例1]右图是M、N两种不含结晶水的固体物质的溶解度曲线。下列说法中正确的是
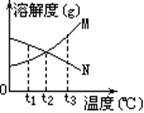 A.t1℃时,N比M的溶解度大
A.t1℃时,N比M的溶解度大
B.温度从t1℃升高到t3℃时,N的饱和溶液中溶质的质量分数将增大
C.M比N的溶解度大
D.N中含有少量M时,可用降温结晶法提纯N
解析:由图可看出,t1℃时N比M的溶解度大, A正确。因N的溶解度随温度的升高而降低,故从t1℃升高到t3℃时N的饱和溶液中溶质的质量分数将减小, B错。温度高于t2℃时M的溶解度大于N,温度低于t2℃时,M的溶解度小于N, C错。N中含有少量M时,可用升温结晶法提纯N,D错。
答案: A
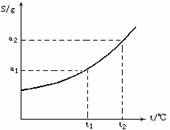 [例2]摩尔质量为M g/mol的某物质的溶解度曲线如图所示,现有t2℃ 300g该物质的溶液,在温度不变时蒸发掉50 g水后,溶液恰好达到饱和,此饱和溶液的密度为ρ g/mL,则饱和溶液的物质的量浓度为____mol/L,若将此饱和溶液降温至t1℃时,析出无水物晶体的质量为______g。
[例2]摩尔质量为M g/mol的某物质的溶解度曲线如图所示,现有t2℃ 300g该物质的溶液,在温度不变时蒸发掉50 g水后,溶液恰好达到饱和,此饱和溶液的密度为ρ g/mL,则饱和溶液的物质的量浓度为____mol/L,若将此饱和溶液降温至t1℃时,析出无水物晶体的质量为______g。
解析:由溶解度曲线可知,在t2时,该物质的溶解度为a2g,
饱和溶液的溶质质量关分数可用下式计算: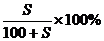
再根据物质的量浓度和溶质质量分数的换算公式,求出溶液的物质的量浓度。
由t2℃的溶解度数据可求出溶液的溶质质量分数
=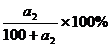 。
。
溶液的物质的量浓度=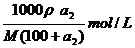
设降温至t1时,析出的晶体的质量为χ
根据公式:100+S(高温)∶S(高温)-S(低温)=高温下饱和溶液质量∶析出晶体质量
(100 +a2)∶(a2-a1)=(300-50)∶χ
χ=250(a2-a1)/(100+a2)g
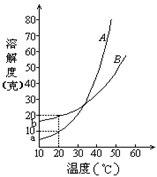 [例3]A、B两种化合物的溶解度曲线如右图。现要用结晶法从A、B混和物中提取A。(不考虑A、B共存时,对各自溶解度的影响。)
(1)取50克混和物,将它溶于100克热水,然后冷却至20℃。若要使A析出而B不析出,则混和物中B的质量百分比(B%)最高不能超过多少?(写出推理及计算过程。)
(2)取W克混和物,将它溶于100克热水,然后冷却至10℃。若仍要使A析出而B不析出,请写出在下列两种情况下,混和物中A的质量百分比(A%)应满足什么关系式。(以W、a、b表示。只需将答案填写在下列横线的空白处.)
当W<a+b时,A%
[例3]A、B两种化合物的溶解度曲线如右图。现要用结晶法从A、B混和物中提取A。(不考虑A、B共存时,对各自溶解度的影响。)
(1)取50克混和物,将它溶于100克热水,然后冷却至20℃。若要使A析出而B不析出,则混和物中B的质量百分比(B%)最高不能超过多少?(写出推理及计算过程。)
(2)取W克混和物,将它溶于100克热水,然后冷却至10℃。若仍要使A析出而B不析出,请写出在下列两种情况下,混和物中A的质量百分比(A%)应满足什么关系式。(以W、a、b表示。只需将答案填写在下列横线的空白处.)
当W<a+b时,A%
当W>a+b时,A% 。
解析:(1)因为在20℃时,A的溶解度为10g,B的溶解度为20g,所以50gA和B的混合物溶于100g热水中,降温至20℃时,要使B不析出,A能析出,则在50g混合物中,B的质量应≤20g,A的质量应≥30g,即在50g混合物中B的质量分数应≤40%。
(2)要使B不析出,B的质量≤b,而A要析出,A的质量应>a。当W<a+b时,只要A>a,即可满足条件,所以A%>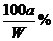 。当W>a+b时,B≤b即可满足条件,所以A%≥
。当W>a+b时,B≤b即可满足条件,所以A%≥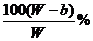
[例4]氯化铁溶液和氢氧化铁胶体具有的共同性质是( )
A.分散系颗粒直径都在1~100nm之间
B.能透过半透膜
C.加热蒸干、灼烧后都有氧化铁生成
D.呈红褐色
解析:溶液中溶质颗粒直径都小于1nm,胶体中胶粒直径都在1~100 nm之间,前者能透过半透膜,后者不能透过半透膜。加热蒸干时,氯化铁水解为氢氧化铁,灼烧后,氢氧化铁分解为氧化铁,氧化铁溶液呈棕黄色,氢氧化铁胶体呈红褐色。
答案:C
1.概念:一种或几种物质分散到另一种物质中形成的混合物叫做分散系。被分散的物质叫做 ,物质分散于其中的物质叫做 。
3.胶体的制备:将少量饱和的氯化铁溶液加入沸水中,可制备氢氧化铁胶体。反应方程式如下: 。
思考:各举一例说明胶体特性的应用:
(1)丁达尔效应 (2)电泳现象
(3)不能透过半透膜 (4)吸咐性
2.胶体的性质:胶体的性质主要为 运动、 现象和 。
1.胶体的概念:分散质直径在 之间的分散系。胶体粒子不能通过 ,但能通过 。所以分离胶体与溶液的方法是 。
有关溶液的计算,除了必需掌握溶解度S、溶质的质量分数ω的计算公式外,还必需掌握饱和溶液中,溶解度S、溶质的质量分数ω、物质的量浓度c之间的换算关系:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com