
22.(12分)已知函数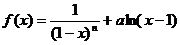 ,其中
,其中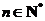 ,
,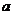 为常数。
为常数。
(1)当 时,求函数
时,求函数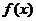 的极值;
的极值;
(2)当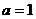 时,证明对任意的正整数
时,证明对任意的正整数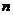 ,当
,当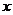 ≥2时,
≥2时,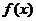 ≤
≤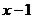 .
.
21.(12分)已知数列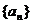 的前
的前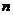 项和
项和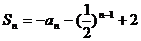 ,(
,(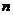 为正整数)
为正整数)
(1)令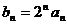 ,求证:数列
,求证:数列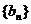 是等差数列,并求数列
是等差数列,并求数列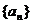 的通项公式;
的通项公式;
(2)令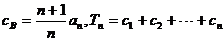 ,试比较
,试比较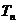 与
与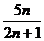 的大小,并予以证明。
的大小,并予以证明。
20.(12分)某地建一座桥,两端的桥墩已建好,这两桥墩相距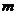 米,余下的工程只需建两端桥墩之间的桥面和桥墩,经测算,一个桥墩工程费用为256万元;距离为
米,余下的工程只需建两端桥墩之间的桥面和桥墩,经测算,一个桥墩工程费用为256万元;距离为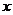 米的相邻两墩之间的桥面工程费用为
米的相邻两墩之间的桥面工程费用为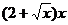 万元,假设桥墩等距离分布,所有桥墩都视为点,且不考虑其它因素,记余下工程费用为
万元,假设桥墩等距离分布,所有桥墩都视为点,且不考虑其它因素,记余下工程费用为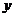 万元。
万元。
(1)试写出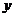 关于
关于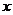 的函数关系式;
的函数关系式;
(2)当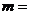 640米,需新建多少个桥墩才能使
640米,需新建多少个桥墩才能使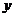 最小。
最小。
19.(12分)设函数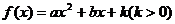 在
在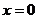 处取得极值,且曲线
处取得极值,且曲线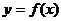 在点
在点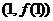 处的切线垂直于线
处的切线垂直于线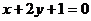
(1)求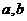 的值;
的值;
(2)若函数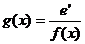 ,讨论
,讨论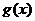 的单调性。
的单调性。
18.(12分)在同一时间段内,有甲乙两个天气预报站相互独立地对本地天气进行预测,根据以往的统计规律,甲预报站对天气预测的准确率为0.8,乙预报站对天气预报的准确率为0.75,求在同一时间段内
(1)甲、乙两个天气预报站至少有一个预报准确的概率;
(2)如果甲站独立预报3次,试写出准确预报次数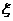 的概率及数学期望。
的概率及数学期望。
17.(10分)求函数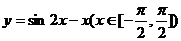 的最大值和最小值。
的最大值和最小值。
16.数列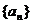 中,
中,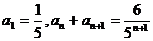 ,则
,则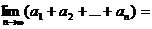 。
。
15.若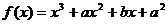 在
在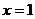 处有极值10时,则
处有极值10时,则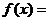 。
。
14.已知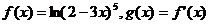 ,则
,则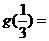 。
。
13.设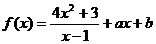 满足
满足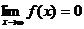 ,则
,则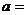 ,
,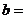 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com