
6.LC振荡电路中,某时刻的磁场方向如图1所示,则 [ ]
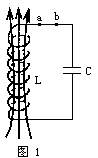
A.若磁场正在减弱,则电容器正在充电,电流由b向α
B.若磁场正在减弱,则电场能正在增大,电容器上板带负电
C.若磁场正在增强,则电场能正在减少,电容器上板带正电
D.若磁场正在增强,则电容器正在充电,电流方向由α向b
5.LC回路振荡电流为零时,有关能量E及电容器电量Q变化,不正确的说法是 [ ]
A.电容C放电完毕,Q为零,E磁最大
B.电容C开始充电,Q将增多,E电最大
C.电容 C开始放电,Q将减少,E磁最大
D.电容C充电完毕,Q将减少,E磁最大
4.LC振荡电路中电容器两板间电压最大时,有 [ ]
A.电感L中的电流最大
B.电感L中的电流为零
C.电容C两板上所带电量最大
D.电容C上所带电量为零
3.在LC回路产生振荡电流的过程中 [ ]
A.振荡电流与电场能同时出现最大值
B.振荡电流与磁场能同时出现最大值
C.电流减弱时,电容器充电
D.电流增强时,电容器充电
2.在LC回路中的电容器刚好放电完毕时,下列说法正确的是 [ ]
A.电场能正向磁场能转化
B.磁场能正向电场能转化
C.电路里电场最强
D.电路里磁场最强
1.在LC回路产生电磁振荡的过程中,下列说法正确的是 [ ]
A.电容器放电完毕时刻,回路中磁场能最小。
B.回路中电流值最大时刻,回路中磁场能最大
C.电容器极板上电荷最多时,电场能最大
D.回路中电流值最小时刻,电场能最小
7.宇宙飞行中的超重和失重
宇宙飞行中的超重和失重通常有两种情况,一是近似做匀速圆周运动的星体或宇航器,万有引力恰好提供了它们所需要的向心力,这是一种完全失重的情况;二就是在宇航器起飞或降落过程,或是由于高度变化引起重力加速度变化,而造成的超重或失重。
例题9.飞船以加速度 (
(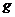 为地球表面的重力加速度)匀加速上升,测得在地面上
为地球表面的重力加速度)匀加速上升,测得在地面上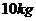 的物体重力为
的物体重力为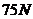 ,由此可求出此时飞船里地的高度为多少?(地球半径
,由此可求出此时飞船里地的高度为多少?(地球半径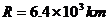 )
)
 解析:设此时飞船离地高度为
解析:设此时飞船离地高度为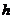 ,该位置处的重力加速度为
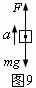
,该位置处的重力加速度为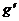 ,如图9所示为该物体的受力情况,其中
,如图9所示为该物体的受力情况,其中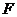 为测力计对物体的作用力,即物体此时的“视重”大小,由牛顿第二定律得
为测力计对物体的作用力,即物体此时的“视重”大小,由牛顿第二定律得
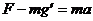
由万有引力定律得

而在地球表面上,有
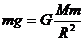
解以上几式,得
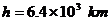
命题解读:这道题目中,飞船加速上升,飞船本身及其里面的物体应该处于超重状态的,但为什么会出现测得的重力小于它在地面上的重力(100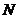 )呢?原因就是该高度处的重力加速度变得比地面上的重力加速度小了!
)呢?原因就是该高度处的重力加速度变得比地面上的重力加速度小了!
6.运用运动学知识求解(任意星体)第一宇宙速度
所谓第一宇宙速度,就是在某一星体表面发射一颗绕该星体表面飞行的卫星所需要的发射速度,即在该星体表面发射卫星所需要的最小速度。
例题8.宇航员在某一星球上以速度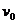 竖直上抛物体,经
竖直上抛物体,经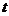
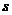 落回手中。已知地球的半径为
落回手中。已知地球的半径为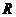 ,该星球的半径为地球半径的一半。那么,至少要用多大的速度沿星球表面抛出物体,它才不至于再落回该星球表面?
,该星球的半径为地球半径的一半。那么,至少要用多大的速度沿星球表面抛出物体,它才不至于再落回该星球表面?
解析:设地球表面的重力加速度为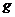 ,该星球表面的重力加速度为
,该星球表面的重力加速度为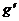 ,则由竖直上抛运动规律和万有引力定律得
,则由竖直上抛运动规律和万有引力定律得
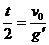
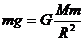
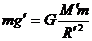
其中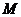 、
、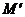 分别为地球和该星球的质量。要想使沿星球表面抛出的物体不至于再落回该星球表面,设最小的速度为
分别为地球和该星球的质量。要想使沿星球表面抛出的物体不至于再落回该星球表面,设最小的速度为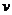 (即第一宇宙速度),则根据圆周运动知识,得
(即第一宇宙速度),则根据圆周运动知识,得
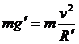
再代入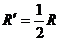 ,解得
,解得
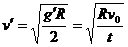
命题解读:这是一道万有引力定律和运动学知识结合的题目,解题的关键就是把联系万有引力定律和运动学知识的“桥梁”--重力加速度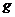 求出来,另外,还要理解第一宇宙速度的真正含义。
求出来,另外,还要理解第一宇宙速度的真正含义。
5.万有引力定律和圆周运动规律的结合
宇宙中星体的运动是比较复杂的,但在研究讨论某些星体的运动时,都是当成最简单、也是最典型的匀速圆周运动来处理。
例题7.某载人飞船在绕地球飞行的第5圈进行变轨,由原来的椭圆轨道变为距地面高度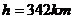 的圆形轨道。已知地球半径
的圆形轨道。已知地球半径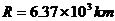 ,地球表面处的重力加速度
,地球表面处的重力加速度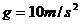 。试推导出飞船在上述圆形轨道上运行的周期
。试推导出飞船在上述圆形轨道上运行的周期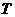 的表达式(用
的表达式(用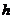 、
、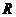 、
、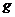 表示),然后计算周期
表示),然后计算周期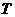 的数值(保留两位有效数字)。
的数值(保留两位有效数字)。
解析:飞船绕地球做近似的匀速圆周运动,需要的向心力由地球对它的万有引力提供,则有
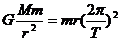
地球表面处的物体的重力等于万有引力,即
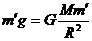
又 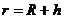
解以上三式的得
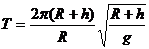
代入数据,得
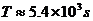
命题解读:这类有关卫星或飞船绕天体做圆周运动的计算问题中,一般只需把握两个方面就可以了,第一个(也是最重要的)就是万有引力恰好提供向心力,第二个则是天体表面物体所受的的重力等于万有引力。
4.圆周运动中的临界问题
直线运动中我们已经做过很多临界状态的分析、判断和求解的问题,在曲线运动中也会遇到“当……时,恰好……”的临界问题。
 例题5.两绳
例题5.两绳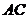 和
和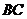 同时系一质量为
同时系一质量为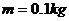 的小球,且
的小球,且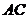 绳长为
绳长为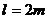 ,两绳都拉直时与竖直方向的夹角分别为
,两绳都拉直时与竖直方向的夹角分别为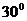 角和
角和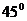 角,如图4所示。当小球以
角,如图4所示。当小球以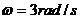 绕
绕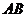 为轴转动时,上、下两绳的拉力分别是多少?
为轴转动时,上、下两绳的拉力分别是多少?
解析:由于两根长度不同,小球绕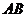 为轴转动的角速度
为轴转动的角速度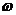 由0逐渐增大时,最先被拉直的应该是绳
由0逐渐增大时,最先被拉直的应该是绳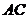 ,当角速度
,当角速度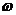 增大到某一数值
增大到某一数值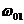 时,会出现绳
时,会出现绳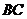 刚好被拉直(绳中无张力)的情况,此时是重力和绳
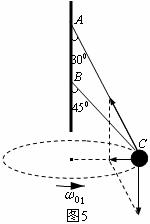
刚好被拉直(绳中无张力)的情况,此时是重力和绳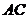 的拉力提供了小球做匀速圆周运动的向心力,如图5所示,由圆周运动知识得
的拉力提供了小球做匀速圆周运动的向心力,如图5所示,由圆周运动知识得
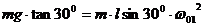
解得 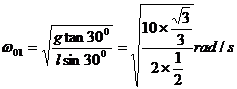
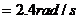
同理可以求得,当角速度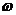 继续增大到某一数值
继续增大到某一数值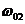 时,又会出现
时,又会出现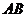 刚好被拉直的情况,则有
刚好被拉直的情况,则有
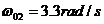
显然,这两个临界状态下的角速度值与题中所给的加速度有如下的关系,即
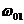 <
<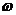 <
<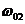
由此可以判断题中所求的是两绳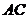 和
和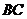 都被拉直并且都存在拉力的情况,设此时两绳
都被拉直并且都存在拉力的情况,设此时两绳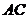 和
和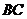 对小球的拉力分别为
对小球的拉力分别为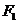 和
和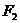 ,如图6所示,则有
,如图6所示,则有
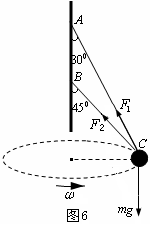
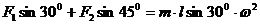
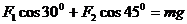
解以上两式,得
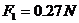 ,
,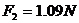
即,绳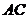 和
和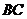 对小球的拉力分别为
对小球的拉力分别为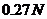 和
和 。
。
命题解读:此题中,由于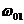 <
<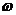 <
<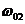 ,所以判断的结果是两绳都被拉直,并且都产生了对小球的拉力。若出现
,所以判断的结果是两绳都被拉直,并且都产生了对小球的拉力。若出现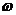 <
<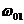 或
或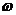 >
>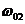 的情况时,两绳
的情况时,两绳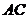 和
和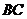 与竖直方向的夹角就将分别小于
与竖直方向的夹角就将分别小于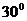 角或大于
角或大于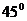 角了,就会出现其中一绳不产生拉力,这时要根据具体的受力分析列出相应的关系式进行求解。
角了,就会出现其中一绳不产生拉力,这时要根据具体的受力分析列出相应的关系式进行求解。
 例题6.如图7所示,一质量
例题6.如图7所示,一质量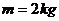 的小球从光滑斜面上某处由静止滚下,斜面底端与一个半径
的小球从光滑斜面上某处由静止滚下,斜面底端与一个半径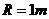 的竖直放置的光滑圆环相接,试求:
的竖直放置的光滑圆环相接,试求:
⑴小球至少应从多高处由静止滚下才能越过圆环的最高点?
⑵若小球从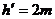 处由静止滚下时将在何处脱离圆环?
处由静止滚下时将在何处脱离圆环?
解析:⑴设小球至少应从高为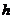 处由静止滚下,如图所示,由机械能守恒定律和圆周运动知识可得
处由静止滚下,如图所示,由机械能守恒定律和圆周运动知识可得
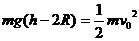
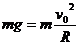
解得 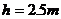
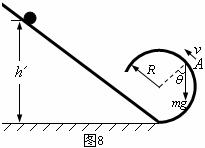 ⑵由于
⑵由于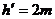 <
<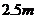 ,所以小球在从圆形轨道的右侧向上滚动的过程中将不会到达圆形轨道的最高点,在到达最高点之前就已经脱离轨道。如图9所示,设小球在
,所以小球在从圆形轨道的右侧向上滚动的过程中将不会到达圆形轨道的最高点,在到达最高点之前就已经脱离轨道。如图9所示,设小球在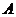 处刚好脱离轨道(对轨道压力为零),此时小球的速度为
处刚好脱离轨道(对轨道压力为零),此时小球的速度为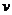 ,由机械能守恒定律和圆周运动知识,得
,由机械能守恒定律和圆周运动知识,得
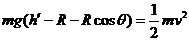
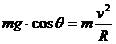
解得 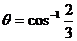
命题解读:此题的第一问中,问“至少应从多高处由静止滚下才能越过圆环的最高点?”,意思就是要求小球刚好到达圆周的最高点,第二问中,轨道对小球压力恰好为零的位置就是小球脱离轨道的地方,这都是临界状态问题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com