5．经济学中有“刘易斯拐点”之说，意指劳动力从无限供给到短缺的临界点。简而言之，在“刘易斯拐点”之前，是人求工作，不涨工资也会有源源不绝的劳动力；在“刘易斯拐点”之后，是工作求人，不涨工资就找不到合适的员工。“刘易斯拐点”对解决目前“用工荒”问题的启示是：　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．处理好效率与公平的关系，缩小工资收入差距

　　　 B．理顺分配关系，提高劳动报酬在初次分配中的比重

　　　 C．发挥市场在资源配置中的基础性作用　

　　　 D．完善社会保障制度，依法维护劳动者权益

4．国务院决定20l0年所有事业单位进行绩效工资改革。事业单位绩效的核心是它所提供的公益性服务的质量和数量，改革的目的是在事业单位建立一种把薪酬分配与公益性服务绩效紧密相连的新的激励约束机制。对事业单位实施绩效工资：　　　　　　　　　　　　　　　　 (　　 )

　　　 ①是对我国现行分配制度的根本性变革　

　　　 ②体现了按劳分配原则

　　　 ③将劳动者付出的劳动数量和质量与个人收入直接联系在一起，有利于激发劳动者的积极性

　　　 ④实现了按劳分配与按生产要素分配的结合

　 　　 A．①②　　　　　　　　　 B．①③　　　　　　　　　 C．②③　　　　　　　　　 D．③④

3．教育部部长袁贵仁表示，2010年全国普通高校毕业生规模达630余万人，加上往届未实现就业的100余万，高校毕业生就业形势十分严峻。如果请你给大学毕业生提出就业建议，最恰当的是：　　　　　　　　　　　　　　 (　　 )

　　　 A．根据个人兴趣、爱好决定选择何种职业　

　　　 B．提高个人技能、素质，主动适应劳动力市场需求

　　　 C．社会有分工，职业有高低，要慎重考虑　

　　　 D．就业形式多样化，可以随机选择职业

2．“因为房子，我们害怕事业；因为房子，我们不敢创业；因为房子，我们被迫啃老；因为房子，我们不敢养育下一代。”80后青年的自嘲表明：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．我们的整体消费水平很低　　 　　　　　　 B．我们的整体物价指数很高

　　　 C．“被消费”成为主要的消费方式　　 　 D．我国的消费结构很不合理

1．我国某企业在国际市场上以6美元/件的价格出售100万件某商品，该企业生产商品的成本是人民币13元/件，如果该企业的个别劳动生产率提高30%，假设结算当日汇率为1美元兑换6．8元人民币，则该企业出售100万件商品可获得利润为人民币多少万元？　　　　　　　　　　　　　　 (　　 )

　　　 A．3080万元　　　 　　　　　　　　　　　　　　　 B．3120万元　　　　

　　　 C．2200万元　　 　　　　　　　　　　　　　　　　 D．2064万元

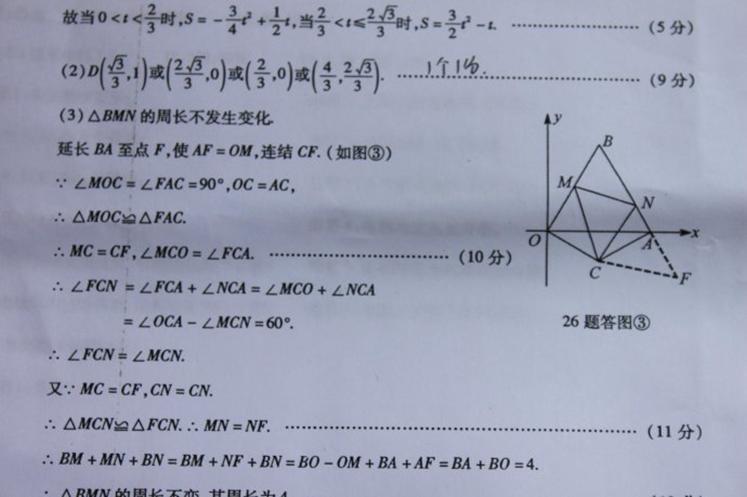
26．已知：如图(1)，在平面直角坐标xOy中，边长为2的等边△OAB的顶点B在第一象限，顶点A在x轴的正半轴上．另一等腰△OCA的顶点C在第四象限，OC＝AC，∠C＝120°．现有两动点P、Q分别从A、O两点同时出发，点Q以每秒1个单位的速度沿OC向点C运动，点P以每秒3个单位的速度沿A→O→B运动，当其中一个点到达终点时，另一个点也随即停止.

(1)求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系，并写出自变量t的取值范围；

(2)在等边△OAB的边上(点A除外)存在点D，使得△OCD为等腰三角形，请直接写出所有符合条件的点D的坐标；

(3)如图(2)，现有∠MCN＝60°，其两边分别与OB、AB交于点M、N，连接MN．将∠MCN绕着C点旋转(0°＜旋转角＜60°)，使得M、N始终在边OB和边AB上．试判断在这一过程中，△BMN的周长是否发生变化？若没有变化，请求出其周长；若发生变化，请说明理由．

25．今年我国多个省市遭受严重干旱，受旱灾的影响，4月份，我市某蔬菜价格呈上升趋势，其前四周每周的平均销售价格变化如下表：

进入5月，由于本地蔬菜的上市，此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克，且y与周数x的变化情况满足二次函数y＝－ x²+bx+c.

(1)请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x 的函数关系式，并求出5月份y与x的函数关系式；

(2)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m＝x+1.2，5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m＝x+2．试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大？且最大利润分别是多少？

(3)若5月份的第2周共销售100吨此种蔬菜．从5月份的第3周起，由于受暴雨的影响，此种蔬菜的可供销量将在第2周销量的基础上每周减少a %，政府为稳定蔬菜价格，从外地调运2吨此种蔬菜，刚好满足本地市民的需要，且使此种蔬菜的销售价格比第2周仅上涨0.8 a %．若在这一举措下，此种蔬菜在第3周的总销售额与第2周刚好持平，请你参考以下数据，通过计算估算出a的整数值．

(参考数据：37²＝1369，38²＝1444，39²＝1521，40²＝1600，41²＝1681)

24． 已知：如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90°．点E是DC的中点，过点E作DC的垂线交AB于点P，交CB的延长线于点M．点F在线段ME上，且满足CF＝AD，MF＝MA．

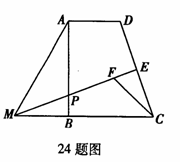(1)若∠MFC＝120°，求证：AM＝2MB；

(2)求证：∠MPB＝90°－ ∠FCM．

23．在“传箴言”活动中，某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计，并制成了如下两幅不完整的统计图：

(1)求该班团员在这一个月内所发箴言的平均条数是多少？并将该条形统计图补充完整；

(2)如果发了3条箴的同学中有两位同学，发了4条箴言的同学中有三位女同学． 现要从发了3条箴和4条箴言的同学中分别选出一位参加该校团委组织的“箴言”活动总结会，请你用列表法或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．

22．已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A(－2，0)，与反比例函数在第一象限内的图象的交于点B(2，n)，连结BO，若S_△AOB＝4．

(1)求该反比例函数的解析式和直线AB的解析式；

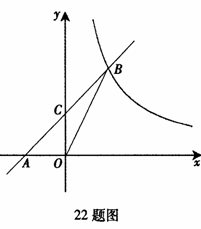(2)若直线AB与y轴的交点为C，求△OCB的面积．