
2.某物体一天中的温度T(单位:摄氏度)是时间t(单位:小时)的函数T(t)=t3-3t+60,t=0表示中午12:00,则下午3时的温度为 ( )
A.8℃ B.18℃ C.78℃ D.112℃
1.某村对200户家庭的生活水平进行调查,其中一项的统计结果是:有彩电的180户,有电冰箱的186户,两样都有的168户,则彩电和电冰箱至少有一样的户数是 ( )
A.197 B.198 C.199 D.200
22. 解:(1)∵f(x)=-x-ln(-x),f´(x)= -1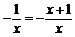 ,
,
∴当-e<x<-1时, f´(x)<0,此时f(x)单调递减,当-1<x<0时,f´(x)>0,
此时f(x) 单调递增,∴f(x)的极小值为f(-1)=1.
(2)∵f(x)的极小值即f(x)在[-e,0)上的最小值为1,∴| f(x)|min=1,
令h(x)=g(x)+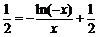 , 又∴h´(x)=
, 又∴h´(x)=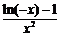 ,∴当-e<x<0时, h´(x) <0,且h(x)在x=-e处连续
,∴当-e<x<0时, h´(x) <0,且h(x)在x=-e处连续
∴h(x)在[-e,0)上单调递减,∴h(x)max=h(-e)=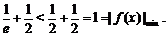
∴当x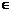 [-e,0)时,
[-e,0)时, 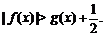

21. 解:(Ⅰ)由
 得
得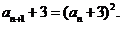
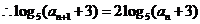 ,即
,即 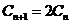 ,
,
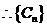 是以2为公比的等比数列
是以2为公比的等比数列
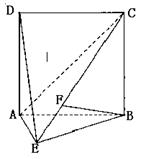 (Ⅱ) 又
(Ⅱ) 又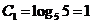
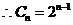 即
即 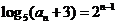 ,
, 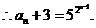
故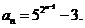
(Ⅲ)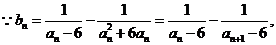 =
=
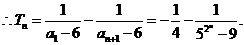
又
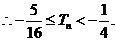
20.解: (1)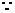 直二面角D-AB-E
直二面角D-AB-E
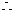 平面ABCD
平面ABCD 平面ABE
平面ABE
又 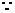 四边形ABCD为正方形
四边形ABCD为正方形
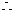 CB
CB AB
AB 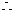 CB
CB 平面ABE
平面ABE
又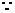 BF
BF 平面ACE
平面ACE 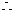 BF
BF AE
AE
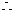 AE
AE 平面BCE
平面BCE
(2)作FO AC连结OB
AC连结OB
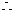 AC
AC 平面OFB
平面OFB
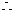 AC
AC OB
OB 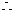
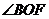 为二面角的平面角
为二面角的平面角
AE=BE=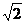 EC=
EC=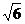
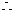 BF=
BF= OB=
OB=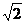
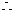 OF=
OF=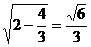
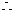 cos
cos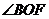 =
=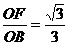 所以二面角B-AC-E的余弦值为
所以二面角B-AC-E的余弦值为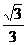 .
.
(3) 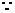
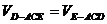
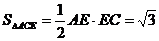
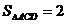
又因为E到平面ACD的距离为1 所以D到平面ACE的距离为 .
.
19.解:(1)原式可化为
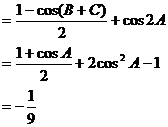
(2)2
所以 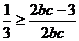
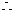
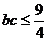 又
又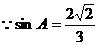
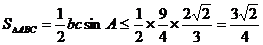 所以三角形ABC的面积最大值为
所以三角形ABC的面积最大值为 .
.
18.解:
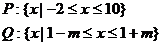 由题知p是q的充分非必要条件 所以
由题知p是q的充分非必要条件 所以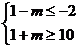 所以
所以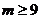
17. 解:圆心O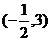 圆心到直线的距离
圆心到直线的距离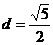
又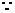
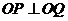 半径
半径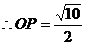
又因为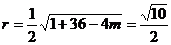 所以
所以 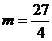
22.(本小题满分12分)已知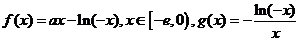 其中
其中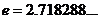 是自然数的底数。
是自然数的底数。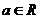
(1)若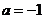 ,求
,求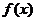 的极值;
的极值;
(2)求证:在(1)的条件下,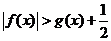 ;
;
(3)是否存在实数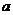 ,使
,使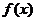 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出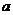 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.
高三月考数学理科试题
21. (本小题满分12分)数列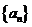 :满足
:满足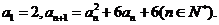
(Ⅰ) 设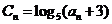 ,求证
,求证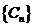 是等比数列;
是等比数列;
(Ⅱ) 求数列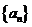 的通项公式;
的通项公式;
(Ⅲ)设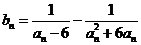 ,数列
,数列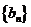 的前
的前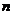 项和为
项和为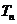 ,求证:
,求证: 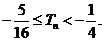
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com