1.工人月工资y(元)依劳动生产率x(千元)变化的回归方程为y＝50+80x，下列判断正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．劳动生产率为1 000元时，工资为130元

B．劳动生产率提高1 000元时，工资平均提高80元

C．劳动生产率提高1 000元时，工资平均提高130元

D．当月工资为210元，劳动生产率为2 000元

解析：由回归方程知，直线的斜率为80.

答案：B

7．已知回归方程y＝4.4x+838.19，则可估计x与y的增长速度之比约为________．

解析：x与y的增长速度之比即为回归方程的斜率的倒数＝＝.

6.对有线性相关关系的两个变量建立的回归直线方程y＝a+bx中，回归系数b(　)

A．可以小于0　 　　B．大于0　　　 C．能等于0　　 　D．只能小于0

解析：因为b＝0时，r＝0，这时不具有线性相关关系，但b能大于0也能小于0.

答案：A

5．在一段时间内，某种商品价格x(万元)和需求量y(吨)之间的一组数据为：

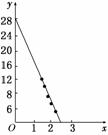
(1)画出散点图；

(2)求出y对x的线性回归方程，并在(1)的散点图中画出它的图像；

(3)如果价格定为1.9万元，预测需求量大约是多少(精确到0.01吨)?

解：(1)散点图，如图．

(2)采用列表的方法计算a与回归系数b.

序号

＝×9＝1.8，＝×37＝7.4，

b＝＝－11.5，

a＝7.4+11.5×1.8＝28.1，

y对x的线性回归方程为

y＝a+bx＝28.1－11.5x.

(3)当x＝1.9时，

y＝28.1－11.5×1.9＝6.25，

所以价格定为1.9万元时，需求量大约是6.25吨．

4．下表是某厂1-4月份用水量(单位：百吨)的一组数据，

由其散点图知，用水量y与月份x之间有较好的线性相关关系，其线性回归方程是y＝－0.7x+a，则a＝________.

解析：＝2.5，＝3.5，

∴a＝－b＝3.5－(－0.7)×2.5＝5.25.

答案：5.25

3.以下是两个变量x和y的一组数据：

则这两个变量间的线性回归方程为　　　　　　　　　　　　　　　 (　)

A．y＝x² 　　　　　　　　B．y＝

C．y＝9x－15　 　　　　　　D．y＝15x－9

解析：根据数据可得＝4.5，＝25.5，

＝204，_iy_i＝1 296.

b＝＝＝9，

a＝－b＝25.5－9×4.5＝－15.

∴y＝9x－15.

答案：C

2．给出下列关系：

①正方形的边长与面积之间的关系；

②某化妆品的销售量与广告宣传费之间的关系；

③人的身高与视力之间的关系；

④雾天的能见度与交通事故的发生率之间的关系；

⑤学生与其学号之间的关系．

其中具有相关关系的是________．

解析：①正方形的边长与面积之间的关系是函数关系；

②化妆品的销售量与广告宣传费之间的关系不是严格的函数关系，但是具有相关性，因而是相关关系；

③人的身高与视力之间的关系既不是函数关系，也不是相关关系；

④能见度与交通事故的发生率之间具有相关关系；

⑤学生与其学号之间的关系是一种确定的对应关系．

综合以上可知，②④具有相关关系，而①⑤是确定性的函数关系．

答案：②④

1.下列变量之间的关系是函数关系的是　　　　　　　　　　　　　　　　 (　)

A．已知二次函数y＝ax²+bx+c，其中，a，c是已知常数，取b为自变量，因变量是这个函数的判别式Δ＝b²－4ac

B．光照时间和果树亩产量

C．降雪量和交通事故发生率

D．每亩施用肥料量和粮食亩产量

解析：由函数关系和相关关系的定义可知，①中Δ＝b²－4ac，因为a、c是已知常数，b为自变量，所以给定一个b的值，就有唯一确定的Δ与之对应，所以Δ与b之间是一种确定的关系，是函数关系．②③④中两个变量之间的关系都是随机的、不确定的，所以不是函数关系．

答案：A

7．(2009·江苏高考)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习，每人投10次，投中的次数如下表：

则以上两组数据的方差中较小的一个为s²＝________.

解析：由题中表格得，甲班：平均数_甲＝7，

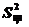＝(1²+0²+0²+1²+0²)＝；

乙班：_乙＝7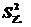，＝(1²+0²+1²+0²+2²)＝.

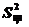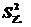∵＜，∴两组数据中方差较小的为s²＝＝.

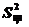6.(2009·四川高考)设矩形的长为a，宽为b，其比满足b：a＝≈0.618，这种矩形给人　　

以美感，称为黄金矩形．黄金矩形常应用于工艺品设计中．下面是某工艺品厂随机抽

取两个批次的初加工矩形宽度与长度的比值样本：

甲批次：0.598　0.625　0.628　0.595　0.639

乙批次：0.618　0.613　0.592　0.622　0.620

根据上述两个样本来估计两个批次的总体平均数，与标准值0.618比较，正确结论是

(　)

A．甲批次的总体平均数与标准值更接近

B．乙批次的总体平均数与标准值更接近

C．两个批次总体平均数与标准值接近程度相同

D．两个批次总体平均数与标准值接近程度不能确定

解析：_甲＝

＝0.617，

_乙＝＝0.613，

∴_甲与0.618更接近．

答案：A