(2010年临沂质检)改革开放以来，我国国有企业在区域经济增长中的比例不断下降。下图为部分省级行政区国有企业总产值的比例(1990年)及其变化(1990~1997年)图，读图回答1~2题。　

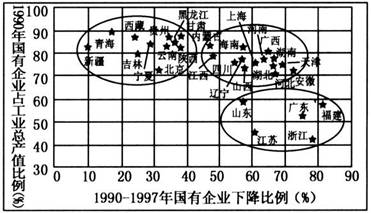
1.下列国有企业发展状况属于“高比例、高下降”类的一组省级行政区是　　　 (　　　 )

A.川、豫、湘　　　　　　　　　 B.鲁、苏、粤　

C.青、藏、内蒙古　　　　　　　 D.吉、京、滇

2.国有企业发展属于“低比例、高下降”类的省区，其共同的区位优势是　　　 (　　　 )

A.地势平坦，企业占地容易获得　

B.处于沿海位置，较容易吸引外资　

C.内河航运发达，便于原料运进　

D.省内劳动力丰富，不需外来迁入

2．设A、B为两个事件，若事件A和B同时发生的概率为，在事件A发生的条件下，事件B发生的概率为，则事件A发生的概率为________________．

解析：由题意知，P(AB)＝，P(B|A)＝，

∴P(A)＝＝＝.

1.已知盒中装有3只螺口与7只卡口灯泡，这些灯泡的外形与功率都相同且灯口向下放着，现需要一只卡口灯泡，电工师傅每次从中任取一只并不放回，则在他第1次抽到的是螺口灯泡的条件下，第2次抽到的是卡口灯泡的概率为　　　　　　　　　　　　 (　)

A. 　　　　　　B.　　　　　　　 C.　 　　　　　D.

解析：设事件A为“第1次抽到是螺口灯泡”，事件B为“第2次抽到是卡口灯泡”，则P(A)＝，P(AB)＝×＝＝.在已知第1次抽到螺口灯泡的条件下，第2次抽到卡口灯泡的概率为P(B|A)＝＝＝.

答案：D

10.抛掷2颗骰子，所得点数之和X是一个随机变量，则P(X≤4)＝________.

解析：相应的基本事件空间有36个基本事件，其中X＝2对应(1,1)；X＝3对应(1,2)，(2,1)；X＝4对应(1,3)，(2,2)，(3,1)．

所以P(X≤4)＝P(X＝2)+P(X＝3)+P(X＝4)

＝++＝.

9．(2009·天津高考改编)在10件产品中，有3件一等品，4件二等品，3件三等品，从这10件产品中任取3件，求：

(1)取出的3件产品中一等品件数X的分布列；

(2)取出的3件产品中一等品件数多于二等品件数的概率．

解：(1)由于从10件产品中任取3件的结果数为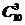，从10件产品中任取3件，其中恰有k件一等品的结果数为C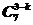，那么从10件产品中任取3件，其中恰有k件一等品的概率为P(X＝k)＝，k＝0,1,2,3.

所以随机变量X的分布列是

(2)设“取出的3件产品中一等品件数多于二等品件数”为事件A，“恰好取出1件一等品和2件三等品”为事件A₁，“恰好取出2件一等品”为事件A₂，“恰好取出3件一等品”为事件A₃.由于事件A₁，A₂，A₃彼此互斥，且A＝A₁+A₂+A₃，而

P(A₁)＝＝，P(A₂)＝P(X＝2)＝，

P(A₃)＝P(X＝3)＝，

∴取出的3件产品中一等品件数多于二等品件数的概率为

P(A)＝P(A₁)+P(A₂)+P(A₃)＝++＝.

8．在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用X表示这10个村庄中交通不方便的村庄数，下列概率中等于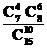的是　　　　　　　　　　 (　)

A．P(X＝2)　 　　　　　　　　　B．P(X≤2)

C．P(X＝4)　 　　　　　　　　　D．P(X≤4)

解析：15个村庄中，7个村庄交通不方便，8个村庄交通方便，CC表示选出的10个村庄中恰有4个交通不方便、6个交通方便的村庄，故P(X＝4)＝.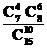

答案：C

7.一盒中有12个乒乓球，其中9个新的，3个旧的，从盒中任取3个球来用，用完后装回盒中，此时盒中旧球个数X是一个随机变量，其分布列为P(X)，则P(X＝4)的值为(　)

A. 　　　　　B.　　　　　　　 C. 　　　　　D.

解析：由题意取出的3个球必为2个旧球1个新球，

故P(X＝4)＝＝.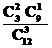

答案：C

6．设一汽车在前进途中要经过4个路口，汽车在每个路口遇到绿灯(允许通行)的概率为，遇到红灯(禁止通行)的概率为.假定汽车只在遇到红灯或到达目的地时才停止前进，X表示停车时已经通过的路口数，求：

(1)X的分布列；

(2)停车时最多已通过3个路口的概率．

解：(1)X的所有可能值为0,1,2,3,4.用A_k表示事件“汽车通过第k个路口时不停(遇绿灯)”，

则P(A_k)＝(k＝1,2,3,4)，且A₁，A₂，A₃，A₄独立．

故P(X＝0)＝P(₁)＝；

P(X＝1)＝P(A₁·₂)＝×＝；

P(X＝2)＝P(A₁·A₂·₃)＝()²＝；

P(X＝3)＝P(A₁·A₂·A₃·₄)＝()³＝；

P(X＝4)＝P(A₁·A₂·A₃·A₄)＝()⁴＝.

从而X有分布列：

(2)P(X≤3)＝1－P(X＝4)＝1－＝.

即停车时最多已通过3个路口的概率为.

5.一袋中装有6个同样大小的黑球，编号为1,2,3,4,5,6，现从中随机取出3个球，以X表示取出球的最大号码，求X的分布列．

解：随机变量X的取值为3,4,5,6.

P(X＝3)＝＝；

P(X＝4)＝＝；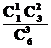

P(X＝5)＝＝；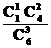

P(X＝6)＝＝.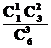

故随机变量X的分布列为：

4．由于电脑故障，使得随机变量X的分布列中部分数据丢失(以“x，y”代替)，其表如下：

则丢失的两个数据依次为______________．

解析：由于0.20+0.10+0.x5+0.10+0.1y+0.20＝1，

得0.x5+0.1y＝0.40，于是两个数据分别为2,5.

答案：2,5