7.(★★★★)如图，已知三棱柱A1B1C1-ABC的底面是边长为2的正三角形，侧棱A1A与AB、AC均成45°角，且A1E⊥B1B于E，A1F⊥CC1于F.

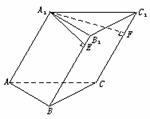
(1)求点A到平面B1BCC1的距离；

(2)当AA1多长时，点A1到平面ABC与平面B1BCC1的距离相等.

6.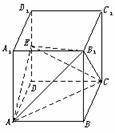(★★★★★)已知正四棱柱ABCD-A1B1C1D1，点E在棱D1D上，截面EAC∥D1B且面EAC与底面ABCD所成的角为45°,AB=a,求：

(1)截面EAC的面积；

(2)异面直线A1B1与AC之间的距离；

(3)三棱锥B1-EAC的体积.

5.(★★★★★)在长方体ABCD-A1B1C1D1中，AB=4，BC=3，CC1=2，如图：

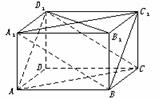
(1)求证：平面A1BC1∥平面ACD1；

(2)求(1)中两个平行平面间的距离；

(3)求点B1到平面A1BC1的距离.

4.(★★★★)如右上图，ABCD与ABEF均是正方形，如果二面角E-AB-C的度数为

30°，那么EF与平面ABCD的距离为_________.

3.(★★★★)如左下图，空间四点A、B、C、D中，每两点所连线段的长都等于a，动点P在线段AB上，动点Q在线段CD上，则P与Q的最短距离为_________.

2.(★★★★)三棱柱ABC-A1B1C1中，AA1=1，AB=4，BC=3，∠ABC=90°,设平面A1BC1与平面ABC的交线为l，则A1C1与l的距离为(　　 )

A.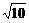　　　　　　　　　　　　 B. 　　　　　　　　　　　　　　 C.2.6　　　　　　　　　　　　　 D.2.4

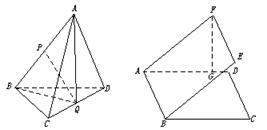
1.(★★★★★)正方形ABCD边长为2，E、F分别是AB和CD的中点，将正方形沿EF折成直二面角(如图)，M为矩形AEFD内一点，如果∠MBE=∠MBC，MB和平面BCF所成角的正切值为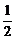，那么点M到直线EF的距离为(　　 )

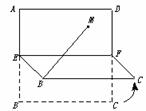
8.(★★★★★)设D是△ABC的BC边上一点，把△ACD沿AD折起，使C点所处的新位置C′在平面ABD上的射影H恰好在AB上.

(1)求证：直线C′D与平面ABD和平面AHC′所成的两个角之和不可能超过90°；

(2)若∠BAC=90°，二面角C′-AD-H为60°，求∠BAD的正切值.

7.(★★★★★)一副三角板拼成一个四边形ABCD，如图，然后将它沿BC折成直二面角.

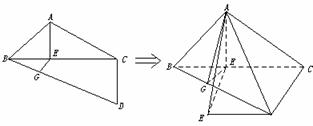
(1)求证：平面ABD⊥平面ACD；

(2)求AD与BC所成的角；

(3)求二面角A-BD-C的大小.

6.(★★★★)设△ABC和△DBC所在的两个平面互相垂直，且AB=BC=BD，∠ABC=

∠DBC=120°

求：(1)直线AD与平面BCD所成角的大小；

(2)异面直线AD与BC所成的角；

(3)二面角A-BD-C的大小.