
22.(本小题满分12分)
如图,在直角坐标系中,点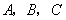 的坐标分别为
的坐标分别为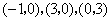 ,过
,过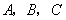 三点的抛物线的对称轴为直线
三点的抛物线的对称轴为直线 为对称轴
为对称轴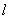 上一动点.
上一动点.
(1) 求抛物线的解析式;
(2) 求当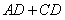 最小时点
最小时点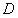 的坐标;
的坐标;
(3) 以点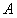 为圆心,以
为圆心,以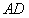 为半径作
为半径作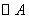 .
.
①证明:当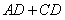 最小时,直线
最小时,直线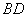 与
与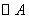 相切.
相切.
②写出直线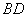 与
与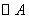 相切时,
相切时,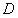 点的另一个坐标:___________.
点的另一个坐标:___________.
21. (本小题满分10分)
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(1)当MN和AB之间的距离为0.5米时,求此时△EMN的面积;
(2)设MN与AB之间的距离为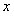 米,试将△EMN的面积S(平方米)表示成关于x的函数;
米,试将△EMN的面积S(平方米)表示成关于x的函数;
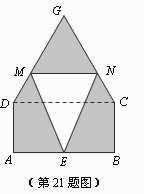
(3)请你探究△EMN的面积S(平方米)有无最大值,若有,请求出这个最大值;若没有,请说明理由.
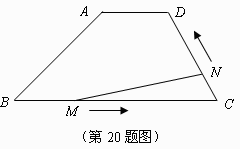
20.(本小题满分9分)
如图,在梯形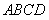 中,
中, 动点
动点 从
从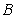 点出发沿线段
点出发沿线段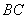 以每秒2个单位长度的速度向终点
以每秒2个单位长度的速度向终点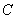 运动;动点
运动;动点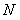 同时从
同时从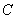 点出发沿线段
点出发沿线段 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点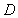 运动.设运动的时间为
运动.设运动的时间为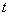 秒.
秒.
(1)求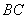 的长.
的长.
(2)当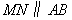 时,求
时,求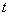 的值.
的值.
(3)试探究: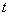 为何值时,
为何值时,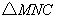 为等腰三角形.
为等腰三角形.
19.(本小题满分9分)
某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用6天;
(3)若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
18.(本小题满分8分)
如图,路灯( 点)距地面8米,身高1.6米的小明从距路灯的底部(
点)距地面8米,身高1.6米的小明从距路灯的底部(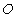 点 )20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
点 )20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
17.(本小题共两小题,每小题满分4分,共8分)
(1).解不等式组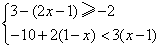
(2).化简: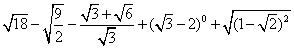
16.在四边形ABCD中,已知AB不平行CD, AC、BD相交于点O,∠ABD=∠ACD,请你添加一个条件:
,使得加上这个条件后能够推出AD∥BC且AB=CD.
15.若关于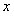 的一元二次方程
的一元二次方程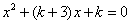 的一个根是
的一个根是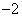 ,则另一个根是__ ____.
,则另一个根是__ ____.
14.函数y=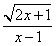 中,自变量x的取值范围是
.
中,自变量x的取值范围是
.
13.在直径为10cm的圆中,弦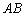 的长为8cm,则它的弦心距为
cm.
的长为8cm,则它的弦心距为
cm.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com