
9.解:前 项一共连续出现了
项一共连续出现了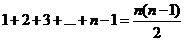 个奇数,
个奇数,
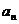 是由第
是由第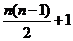 个奇数开始,一直连续的
个奇数开始,一直连续的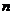 个奇数相加,
个奇数相加,
得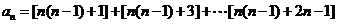
而
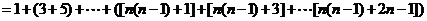

这是一个总共有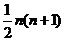 项的等差数列,
项的等差数列,
即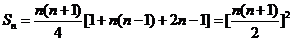 .
.
9.求数列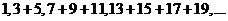 的前
的前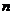 项和.
项和.
8.解: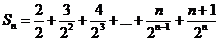 ,
,
 ,
,
相减得: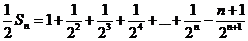 ,
,
即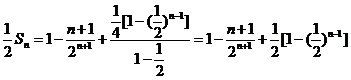 ,
,
得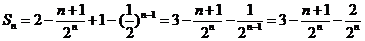 ,
,
即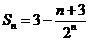 .
.
8.求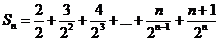 .
.
7.解: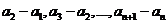 组成首项与公差均为
组成首项与公差均为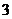 的等差数列,
的等差数列,
即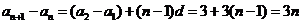 ,
,
得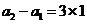 ,
,
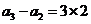 ,
,
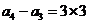 ,
,
.
.
.
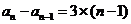
累加得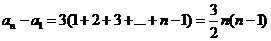 ,
,
得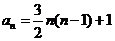 .
.
7.已知一个数列的首项是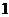 ,从第二项起,依次后项减去前项,所得的差组成首项与
,从第二项起,依次后项减去前项,所得的差组成首项与
公差均为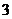 的等差数列,求
的等差数列,求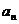 .
.
6.(1)证明: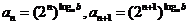 ,
,
则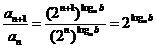 为常数,
为常数,
所以该数列是等比数列;
(2)解: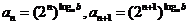 ,
,

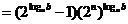 ,
,
因为该数列是等差数列,则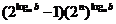 为常数,
为常数,
即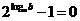 ,得
,得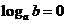 ,即
,即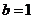 .
.
6.已知数列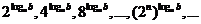 ,其中
,其中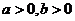 ,且
,且 .
.
(1)求证:该数列是等比数列;
(2)若它是等差数列,求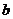 .
.
5.(1)证明:因为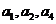 成等比数列,得
成等比数列,得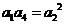 ,
,
即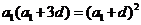 ,得
,得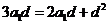 ,即
,即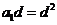 ,
,
而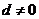 ,得
,得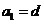 ;
;
(2)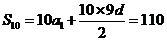 ,由(1)得
,由(1)得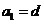 ,
,
即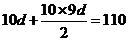 ,得
,得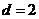 ,
,
数列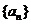 的通项公式
的通项公式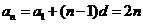 ,即
,即 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com