
5.(09陕西11)
. Gun control is a subject Americans have argued for a long time.
A. of which B. with which C. about which D. into which
答案 C
解析 考查定语从句,先行词是Gun control,指物,关系词在从句中做介词的宾语,介词前置,介词与从句动词构成搭配argue about sth.,选C。
4.(09天津5)
A person ______ e-mail account is full won’t be able to send or receive any e-mails.
A. who B. whom C. whose D. whoever
答案 C
3.(09江苏23)
Because of the financial crisis, days are gone _ _ local 5-star hotels charged 6,000 yuan for one night.
A. if B. when C. which D. since
答案 B
解析 由于金融危机,当地五星级酒店一晚收费6000元的日子不复存在了。when引导的从句做days的定语。
2.(09宁夏海南28)
She brought with her three friends, none of I had ever met before.
A. them B. who
C. whom D. these
答案 C
解析 考查定语从句中的非限制性定语从句。句意为:她带着她的三个朋友,他们三个中没有一个人我曾见过。表示“部分的词语+of+关系代词” 在非限制性定语从句指人只能用whom。
2009年高考题
1.(09山东24)
Whenever I met her, _________ was fairly often, she greeted me with a sweet smile.
A. who B. which C. when D. that
答案 B
解析 本题考查连词的用法,非限制性定语从句,指代前面一个句子,故用which.
20.(Ⅰ)解法一:由题意知,ε的可能取值为0,1,2,3,且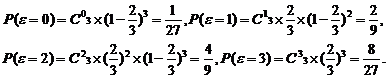
所以ε的分布列为
|
ε |
0 |
1 |
2 |
3 |
|
P |
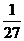 |
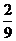 |
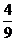 |
 |
ε的数学期望为Eε=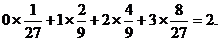
解法二:根据题设可知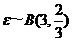
因此ε的分布列为

(Ⅱ)解法一:用C表示“甲得2分乙得1分”这一事件,用D表示“甲得3分乙得0分”这一事件,所以AB=C∪D,且C、D互斥,又
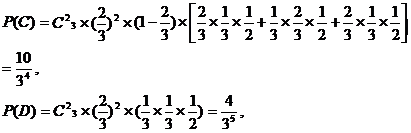
由互斥事件的概率公式得
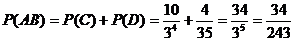
 解法二:用Ak表示“甲队得k分”这一事件,用Bk表示“已队得k分”这一事件,k=0,1,2,3由于事件A3B0,A2B1为互斥事件,故P(AB)=P(A3B0∪A2B1)=P(A3B0)+P(A2B1).
解法二:用Ak表示“甲队得k分”这一事件,用Bk表示“已队得k分”这一事件,k=0,1,2,3由于事件A3B0,A2B1为互斥事件,故P(AB)=P(A3B0∪A2B1)=P(A3B0)+P(A2B1).
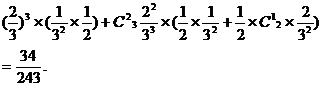
19.(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件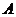 ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件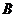 .由于事件
.由于事件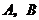 相互独立,且
相互独立,且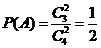 ,
,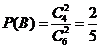 .
.
故取出的4个球均为黑球的概率为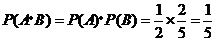 .
.
(Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件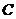 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件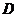 .由于事件
.由于事件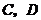 互斥,
互斥,
且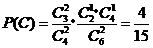 ,
,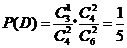 .
.
故取出的4个球中恰有1个红球的概率为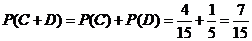 .
.
(Ⅲ)解: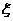 可能的取值为
可能的取值为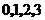 .由(Ⅰ),(Ⅱ)得
.由(Ⅰ),(Ⅱ)得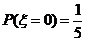 ,
,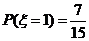 ,
,
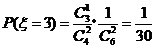 .从而
.从而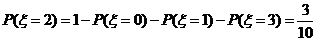 .
.
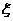 的分布列为
的分布列为
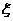 |
0 |
1 |
2 |
3 |
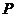 |
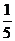 |
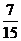 |
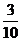 |
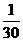 |
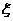 的数学期望
的数学期望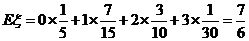 .
.
18.[答案]:(I)基本事件总数为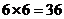 ,
,
若使方程有实根,则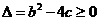 ,即
,即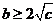 。
。
当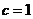 时,
时,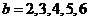 ; 当
; 当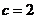 时,
时,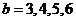 ; 当
; 当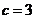 时,
时,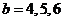 ;
;
当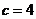 时,
时,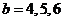 ;
当
;
当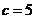 时,
时, ;
当
;
当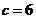 时,
时, ,
,
目标事件个数为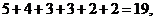
因此方程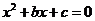 有实根的概率为
有实根的概率为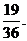
(II)由题意知,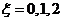 ,则
,则 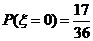 ,
,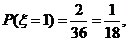
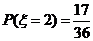 ,
,
故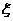 的分布列为
的分布列为
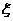 |
0 |
1 |
2 |
|
P |
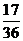 |
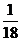 |
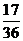 |
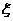 的数学期望
的数学期望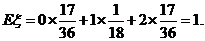
(III)记“先后两次出现的点数中有5”为事件M,“方程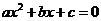 有实根” 为事件N,
有实根” 为事件N,
则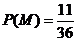 ,
, 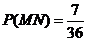 ,
, 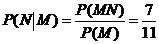 .
.
17.解: (1) 依题意得, ξ的所有可能取值为6,2,1,-2.
ξ=6,2,1,-2分别对应抽取1件产品为一等品、二等品、三等品、次品这四个事件.
所以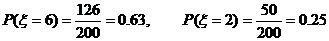 ,
,
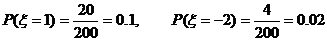 ,
,
所以ξ的分布列为
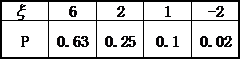
(2) 1件产品的平均利润为Eξ=6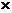 0.63+2
0.63+2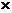 0.25+1
0.25+1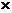 0.1-2
0.1-2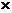 0.02=4.34
0.02=4.34
(3)设三等品率为x,则二等品率为0.29-x,此时ξ的分布列为
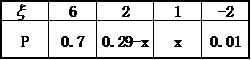
1件产品的平均利润为Eξ=6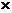 0.7+2
0.7+2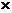 (0.29-x)+x-2
(0.29-x)+x-2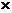 0.01=4.76-x
0.01=4.76-x
令Eξ=4.76-x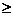 4.73,解得
4.73,解得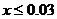 =3%,
=3%,
答:三等品率最多是3%.
16.[解]:记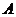 表示事件:进入商场的1位顾客购买甲种商品,
表示事件:进入商场的1位顾客购买甲种商品,
记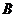 表示事件:进入商场的1位顾客购买乙种商品,
表示事件:进入商场的1位顾客购买乙种商品,
记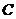 表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种,
表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种,
记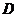 表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种,
表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种,
(Ⅰ)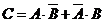
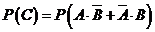
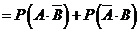
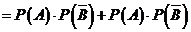
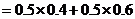
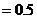
(Ⅱ)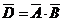
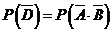

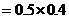
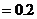 ,
, 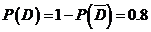
(Ⅲ)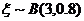 ,故
,故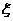 的分布列
的分布列
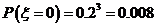 ,
,
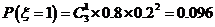
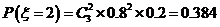 ,
, 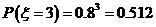
所以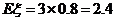
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com