
23.本题满分11分.
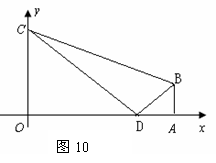 如图10,直角梯形OABC中,OC∥AB,C(0,3),B(4,1),以BC为直径的圆交
如图10,直角梯形OABC中,OC∥AB,C(0,3),B(4,1),以BC为直径的圆交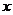 轴于E,D两点(D点在E点右方).
轴于E,D两点(D点在E点右方).
(1)求点E,D 的坐标;
(2)求过B,C,D三点的抛物线的函数关系式;
(3)过B,C,D三点的抛物线上是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.
22.本题满分10分.
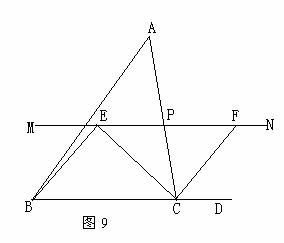
如图9,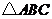 中,点P是边
中,点P是边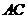 上的一个动点,过P作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
上的一个动点,过P作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:PE=PF;
(2)当点P在边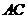 上运动时,四边形BCFE可能是菱形吗?说明理由;
上运动时,四边形BCFE可能是菱形吗?说明理由;
(3)若在AC边上存在点P,使四边形AECF是正方形,且
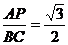 .求此时∠A的大小.
.求此时∠A的大小.
21.本题满分8分.
东艺中学初三(1)班学生到雁鸣湖春游,有一项活动是划船.游船有两种,甲种船每条船最多只能坐4个人,乙种船每条船最多只能坐6个人.已知初三(1)班学生的人数是5的倍数,若仅租甲种船,则不少于12条;若仅租乙种船,则不多于9条.
(1)求初三(1)班学生的人数;
 (2)如果甲种船的租金是每条船10元,乙种船的租金是每条船12元.应怎样租船,才能使每条船都坐满,且租金最少?说明理由.
(2)如果甲种船的租金是每条船10元,乙种船的租金是每条船12元.应怎样租船,才能使每条船都坐满,且租金最少?说明理由.
20. 本题满分8分.
本题满分8分.
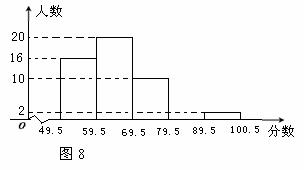
某校九年级有200名学生参加了全国初中数学联合竞赛的初赛,为了了解本次初赛的成绩情况,从中抽取了50名学生, 将他们的初赛成绩(得分为整数,满分为100分)分成五组:第一组49.5-59.5;第二组59.5-69.5;第三组69.5-79.5;第四组79.5-89.5;第五组89.5-100.5.统计后得到图8所示的频数分布直方图(部分). 观察图形的信息,回答下列问题:
观察图形的信息,回答下列问题:
(1)第四组的频数为_________________.(直接填写答案)
(2)若将得分转化为等级,规定:得分低于59.5分评为“D”,59.5-69.5分评为“C”,69.5-89.5分评为“B”,89.5-100.5分评为“A”.那么这200名参加初赛的学生中,参赛成绩评为“D” 的学生约有________个. (直接填写答案)
(3)若将抽取出来的50名学生中成绩落在第四、第五组的学生组成一个培训小组,再从这个培训
小组中随机挑选2名学生参加决赛.用列表法或画树状图法求:挑选的2名学生的初赛成绩恰好都在90分以上的概率.
19. 本题满分8分.
本题满分8分.
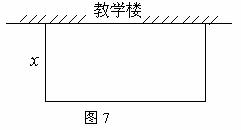
如图7, 东梅中学要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园, 矩形的一边用教学楼的外墙,其余三边用竹篱笆. 设矩形的宽为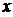 ,面积为
,面积为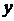 .
.
(1) 求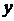 与
与 的函数关系式,并求自变量
的函数关系式,并求自变量 的取值范围;
的取值范围;
(2) 生物园的面积能否达到210平方米?说明理由.
18.本题满分8分.
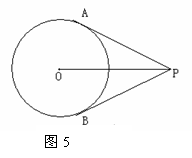
(1)如图5, PA,PB分别与圆O相切于点A,B.求证:PA=PB.
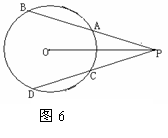
 (2)如图6,过圆O外一点P的两条直线分别与圆O相交于点A、B和C、D.则当___________时,PB=PD.(不添加字母符号和辅助线, 不需证明,只需填上符合题意的一个条件)
(2)如图6,过圆O外一点P的两条直线分别与圆O相交于点A、B和C、D.则当___________时,PB=PD.(不添加字母符号和辅助线, 不需证明,只需填上符合题意的一个条件)
17.本题满分7分.
在平面直角坐标系中,点M的坐标为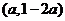 .
.
(1)当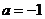 时,点M在坐标系的第___________象限; (直接填写答案)
时,点M在坐标系的第___________象限; (直接填写答案)
(2)将点M向左平移2个单位,再向上平移1个单位后得到点N,当点N在第三象限时,求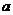 的取值范围.
的取值范围.
16.本题满分7分.
解方程: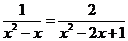 .
.
15.本题满分7分.
计算: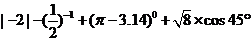 .
.
14. 本题满分7分.
本题满分7分.
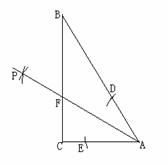
如图4,Rt△ABC中,∠C =90°, ∠A =60°,AC =2.按以下步骤作图: ①以A为圆心,以小于AC长为半径画弧,分别交AC、AB于点E、D; ②分别以D、E为圆心,以大于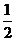 DE长为半径画弧,两弧相交于点P; ③连结AP交BC于点F.那么:
DE长为半径画弧,两弧相交于点P; ③连结AP交BC于点F.那么:
(1)AB的长等于__________;(直接填写答案)
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com