20.(1)△CE B′，用AAS证明略.

　　 (2)∵AB=8，DE=3，根据勾股定理可知，

∴HC=5，B′C=BC=AD=4，

延长HP交AB于M，

∴PM⊥AB ，而折痕AC平分∠BA B′，

∴PM=PG，HM=HP+PM=4.

附加题:

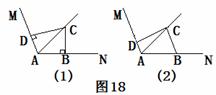
(1) ∵AC平分∠MAN, ∠MAN=120°,

∴∠CAB=∠CAD=60°,

∵∠ABC=∠ADC=90°,

∴∠ACB=∠ACD=30°,

∴AD=AB=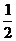AC,

∴AB+AD=AC.

　(2)成立.

　 如图18,过点C分别作AM、AN的垂线,垂足分别为E、F.

∵AC平分∠MAN, ∴CE=CF.

∵∠ABC=∠ADC=180°，∴∠CDE=∠ADC=180°，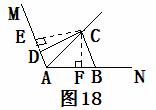

∴∠CDE=∠ABC.

∵∠CED=∠CFB=90°，

∴ΔCED≌ΔCFB，∴ED=FB.

∴AB+AD=(AF+BF)+(AE-FD)=AF+AE.

由(1)知，AF+AE=AC，∴AB+AD=AC.

银行卡号：622893 0001 02512038 1

汪国刚贵州省贵阳市开阳县宅吉中学550307

　身份证号码：520121107312233411

　联系电话：13885146829

19. 连接BD、CD.

　 ∵AD是∠A的平分线，且DE⊥AB,DF⊥AC，

∴DE=DF，

∵MD是BC的垂直平分线，

∴RtΔDEB≌RtΔDFC，

∴BE=CF

18. ∵BO、CO分别是∠ABC与∠ACB的平分线

∴∠DBO=∠CBO，∠ECO=∠BCO，

∵DE//BC

∴∠DOC=∠CBO，∠EOC=∠BCO，

∴∠DBO=∠DOB，∠ECO=∠EOC，

∴DB=DO，EO=EC

∵AD+AE+DE=AD+AE+DO+EO=24

∴AB+AC=2AB=24

∴AB=12

17. ∵AD平分∠BAC，

　　　 ∴∠BAD=∠DAC，

　 又 ∵∠PDA=∠B+∠BAD=∠B+∠DAC，

∵AD的垂直平分AD，

∴PA=PD，

∴∠PAD=∠PDA，而∠PAD=∠PAC+∠DAC，

∴∠B+∠DAC=∠PAC+∠DAC，

∴∠B=∠PAC

16.(1)因为1000m=100 000cm，100 000÷50 000=2(cm)，

　　　　 所以物流中心到公路交叉点A的图上距离为2cm.

　　　 (2)作∠BAC的平分线，且AP=2cm，

如图13所示：

15.(1)连接AP.　

　　∴ PA＝PA　　　　　　　　

　　 ∵

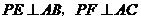
∴∠PEA＝∠PFA＝90°，

∵_，

∴ΔPAE≌ΔPAF(HL).

∴

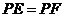
　(2)∵ΔPAE≌ΔPAF，

　　　∴∠PAE＝∠PAF，

　　　∴AP是∠BAC的平分线.

　　　即点P在∠BAC的角平分线上．

9. 这条线段两个端点的距离，一条线段两个端点距离　 　10. 2.5　 11. 2　　 12..7，60　　 13. 36°　 14. 　

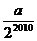
1. D　 2.A　 3.D　 4.B　 5.C　 6.B　 7.C　 8.D

21.(10分)已知∠MAN，AC平分∠MAN.

(1)在图18-1中，若∠MAN=120°，∠ABC=∠ADC=90°，求证：AB+AD=AC；

(2)在图18-2中，若∠MAN=120°，∠ABC=∠ADC=180°，在(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；

答案提示：

20.(10分)如图17，将矩形纸片ABCD沿对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E.

(1)试找出一个与△AED全等的三角形，并加以证明.

(2)若AB=8，DE=3，P为线段AC上的任意一点，PG⊥AE于G，PH⊥EC于H，试求PG+PH的值，并说明理由.

附加题: