10．(15分)已知直线l与两坐标轴围成的三角形的面积为3，分别求满足下列条件的直线l的方程：

(1)过定点A(－3,4)；(2)斜率为.

[解析]　(1)设直线l的方程是y＝k(x+3)+4，它在x轴，y轴上的截距分别是－－3,3k+4，

由已知，得(3k+4)＝±6，

解得k₁＝－或k₂＝－.

直线l的方程为2x+3y－6＝0或8x+3y+12＝0.

(2)设直线l在y轴上的截距为b，则直线l的方程是

y＝x+b，它在x轴上的截距是－6b，

由已知，得|－6b·b|＝6，∴b＝±1.

∴直线l的方程为x－6y+6＝0或x－6y－6＝0.

9．已知直线l的斜率为k，经过点(1，－1)，将直线向右平移3个单位，再向上平移2个单位，得到直线m，若直线m不经过第四象限，则直线l的斜率k的限取值范围是________．

[解析]　依题意可设直线l的方程为y+1＝k(x－1)，即y＝kx－k－1，将直线l向右平移3个单位，得到直线y＝k(x－3)－k－1，再向上平移2个单位得到直线m：y＝k(x－3)－k－1+2，即y＝kx－4k+1.由于直线m不经过第四象限，所以应有，解得0≤k≤.

[答案]　[0，]

8．实数x、y满足3x－2y－5＝0(1≤x≤3)，则的最大值、最小值分别为________、________.

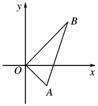
[解析]　设k＝，则表示线段AB：

3x－2y－5＝0(1≤x≤3)上的点与原点的连线的斜率．

∵A(1，－1)，B(3,2)．由右图易知：

_max＝k_OB＝，_min＝k_OA＝－1.

[答案]　－1

7．已知两点M(2，－3)，N(－3，－2)．直线l过P(1,1)且与线段MN相交，则直线l的斜率k的取值范围是________________．

[解析]　如图

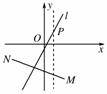
∵k_PN＝，k_PM＝－4.

∴k≥或k≤－4.

[答案]　k≥或k≤－4

6．过点(1,3)作直线l，若经过点(a,0)和(0，b)，且a∈N^*，b∈N^*，则可作出的l的条数为

(　)

A．1　 　　　　　　　　　　　　　　　　　　　　　　 B．2

C．3　 　　　　　　　　　　　　　　　　　　　　　　 D．4

[解析]　解法1：由题意+＝1⇒(a－1)(b－3)＝3.

∵a∈N^*，b∈N^*，

∴有两个解或.

解法2：利用斜率相等知＝⇒(a－1)(b－3)＝3.

以下同解法1.

[答案]　B

5．直线x·cos α+y+2＝0的倾斜角范围是

(　)

A.∪

B.∪

C.

D.

[解析]　由题意知k＝－cos α，∵cos α∈[－1,1]，

∴－≤k≤，由k＝tan α的图象知，

∴0≤α≤或π≤α＜π.

[答案]　B

4．直线x+a²y－a＝0(a>0，a是常数)，当此直线在x，y轴上的截距和最小时，a的值是

(　)

A．1　 　　　　　　　　　　　　　　　　　　　 B．2

C.　 　　　　　　　　　　　　　　　　　　　 D．0

[解析]　方程可化为+＝1，因为a>0，所以截距之和t＝a+≥2，当且仅当a＝，

即a＝1时取等号．

[答案]　A

3．若点A(4,3)，B(5，a)，C(6,5)三点共线，则a的值为

(　)

A．4　 　　　　　　　　　　　　　　　　　　　　　　 B．－4

C．2　 　　　　　　　　　　　　　　　　　　　　　　 D．－2

[解析]　利用k_AB＝k_AC，即＝，得a＝4.

[答案]　A

2．设直线ax+by+c＝0的倾斜角为α，且sin α+cos α＝0，则a，b满足

(　)

A．a+b＝1　 　　　　　　　　　　　　　　　　　 B．a－b＝1

C．a+b＝0　 　　　　　　　　　　　　　　　　　 D．a－b＝0

[解析]　∵sin α+cos α＝0，∴α≠，

∴tan α＝－1，∴a＝b.

[答案]　D

1．已知直线l₁的方向向量为a＝(1,3)，直线l₂的方向向量b＝(－1，k)．若直线l₂经过点(0,5)且l₁⊥l₂，则直线l₂的方程为

(　)

A．x+3y－5＝0　 　　　　　　　　　　　　　　 B．x+3y－15＝0

C．x－3y+5＝0　 　　　　　　　　　　　　　　 D．x－3y+15＝0

[解析]　∵l₂经过(0,5)且方向向量b＝(－1，k)，

∴l₂的方程为y－5＝－kx，又∵l₁的方向向量a＝(1,3)，l₁⊥l₂，

∴－k·3＝－1⇒k＝，即l₂为y－5＝－x，

所求方程为x+3y－15＝0.

[答案]　B