6．(2009年湖北卷)在“家电下乡”活动中，某厂要将100台洗衣机运往邻近的乡镇．现有4辆甲型货车和8辆乙型货车可供使用．每辆甲型货车运输费用400元，可装洗衣机20台；每辆乙型货车运输费用300元，可装洗衣机10台．若每辆车至多只运一次，则该厂所花的最少运输费用为

(　)

A．2 000元　 　　　　　　　　　　　　　　 B．2 200元

C．2 400元　 　　　　　　　　　　　　　　 D．2 800元

[解析]　设需甲型货车x辆，乙型货车y辆，由题意知

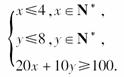
作出其可行域如图．

可知目标函数z＝400x+300y在点A处取最小值，z＝400×4+300×2＝2 200(元)．

[答案]　B

5．(2008年山东卷)设二元一次不等式组，所表示的平面区域为M，使函数y＝a^x(a＞0，a≠1)的图象过区域M的a的取值范围是

(　)

A．[1,3]　 　　　　　　　　　　　　　　　　 B．[2，]

C．[2,9]　 　　　　　　　　　　　　　　　　 D．[，9]

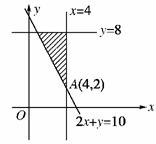
[解析]　作二元一次不等式组的可行域如图所示，由题意得A(1,9)，C(3,8)．

当y＝a^x过A(1,9)时，a取最大值，此时a＝9；

当y＝a^x过C(3,8)时，a取最小值，此时a＝2，∴2≤a≤9.

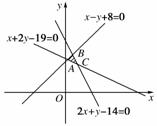
[答案]　C

4．若不等式组表示的平面区域是一个三角形，则a的取值范围是

(　)

A．a＜5　 　　　　　　　　　　　　　　　　 B．a≥8

C．5≤a＜8 　　　　　　　　　　　　　　 D．a＜5或a≥8

[解析]　如图作出可行域，要构成三角形，直线y＝a只能介于y＝5和y＝8两直线间，故5≤a＜8.

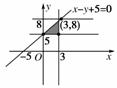
[答案]　C

3．已知实数x，y满足，如果目标函数z＝x－y的最小值为－1，则实数m等于

(　)

A．7　 　　　　　　　　　　　　　　　　　　　 B．5

C．4　 　　　　　　　　　　　　　　　　　　　 D．3

[解析]　将直线y＝x+1与y＝2x－1联立解得A(2,3)，据题意即为最优解，又点A必在直线x+y＝m上，代入求得m＝5.

[答案]　B

2．不等式组表示的平面区域为

(　)

A．四边形及其内部

B．等腰三角形及其内部

C．在第一象限内的一个无界区域

D．不包含第一象限内的点的一个有界区域

[解析]　画出不等式组表示的平面区域如图，易知2x－y+1＝0与x－2y－1＝0关于y＝x对称，与x+y＝1所成角相等，故不等式组表示的平面区域为等腰三角形及其内部．

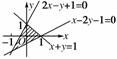
[答案]　B

1．下列各点中，不在x+y－1≤0表示的平面区域的是

(　)

A．(0,0)　　　　　 B．(－1,1)

C．(－1,3)　 　　　　　　　　　　　　　　 D．(2，－3)

[解析]　∵将x＝－1，y＝3代入x+y－1

得－1+3－1＝1>0，

故(－1,3)不在x+y－1≤0表示的平面区域内．

[答案]　C

12．(16分)已知点A(－2,2)及点B(－3，－1)，试在直线l：2x－y－1＝0上，求出符合下列条件的点P：

(1)使|PA|－|PB|为最大；

(2)使|PA|+|PB|为最小；

(3)使|PA|²+|PB|²为最小．

[解析]　(1)因A，B在直线l的同侧，所以直线AB与直线l的交点即为所求．

AB的方程为3x－y+8＝0，与直线l的方程2x－y－1＝0联立解得P(－9，－19)即为所求．

(2)设点B关于直线l的对称点为B′(m，n)，

则

解得B′.

则AB′所在直线与l的交点P即为所求．

(3)设P(x，y)，则|PA|²+|PB|²＝(x+2)²+(y－2)²+(x+3)²+(y+1)²＝2x²+10x+2y²－2y+18＝2x²+10x+2(2x－1)²－2(2x－1)+18＝10x²－2x+22＝10²+.

∴当x＝时，|PA|²+|PB|²取最小值．

此时y＝－，即所求P点坐标为.

11．(15分)等腰直角△ABC的斜边AB所在直线的方程为3x－y＝0，直角边AC所在直线经过点P(4，－2)，且△ABC的面积为10，求直角顶点C的坐标．

[解析]　显然直线x＝4不可能是直角边AC所在的直线．

设直线AC的方程为y+2＝k(x－4)，它与直线AB的夹角为45°.

∴＝tan 45°，即＝1，

解得k＝－2或k＝.

∴直线AC的方程为2x+y－6＝0或x－2y－8＝0.

又△ABC的面积为10，它等于直角顶点C(x，y)到斜边AB的距离d的平方．∴d²＝10，d＝，即＝.

∴直角顶点又在直线3x－y+10＝0或3x－y－10＝0上．

∴直角顶点C的坐标是方程组

的解．

∴直角顶点C的坐标为或

或或.

10．(15分)直线l过原点且与直线x－y－4＝0的夹角为，求直线l的方程．

[解析]　(1)若直线l的斜率存在，设为k，由条件与夹角公式可得＝tan＝，

∴k＝，∴直线l：y＝x.

(2)若直线l的斜率不存在，其方程为x＝0，直线x－y－4＝0的斜率为，故其倾斜角为，

∴两直线的夹角为－＝，x＝0成立．

综上得l的方程为x－y＝0或x＝0.

9．点P(0,1)在直线ax+y－b＝0上的射影是点Q(1,0)，则直线ax－y+b＝0关于直线x+y－1＝0对称的直线方程为______．

[解析]　由已知，有解得

即ax+y－b＝0为x－y－1＝0，

设x－y－1＝0关于x+y－1＝0对称的直线上任一点(x，y)，

点(x，y)关于x+y－1＝0的对称点(x₀，y₀)必在x－y－1＝0上，且，则

代入x－y－1＝0，得x－y－1＝0.

[答案]　x－y－1＝0