
4.曲线y=x2与x2+y2=5的交点是
( )
A.(2,1) B.(±2,1)
C.(2,1)或(2,) D.(±2,1)或(±2,5)
[解析] 解方程组⇒或.
故选B.
[答案] B
3.下列说法正确的是
( )
A.△ABC中,已知A(1,1),B(4,1),C(2,3).则AB边上的高的方程是x=2
B.方程y=x2(x≥0)的曲线是抛物线
C.已知平面上两定点A、B,动点P满足|PA|-|PB|=|AB|,则P点的轨迹是双曲线
D.第一、三象限角平分线的方程是y=x
[解析] 选项A符合曲线与方程的概念(1)曲线上的点的坐标均是这个方程的解,不符合(2)以这个方程的解为坐标的点均是曲线上的点.选项B符合(2)但不符合(1).选项C符合(2)但不符合(1),选项D符合(1)、(2).故选D.
[答案] D
2.若动点P到点F(1,1)和直线3x+y=4的距离相等,则点P的轨迹方程为
( )
A.3x+y-6=0 B.x-3y+2=0
C.x+3y-2=0 D.3x-y+2=0
[解析] 在直线x-3y+2=0上任取一点A(-2,0),
则|AF|==,
点A到3x+y-4=0的距离d==,
∴|AF|=d.故选B.
[答案] B
1.方程|y|-1=表示的曲线是
( )
A.抛物线 B.一个圆
C.两个圆 D.两个半圆
[解析] 原方程等价于
即或
[答案] D
12.(16分)某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
|
|
产品A(件) |
产品B(件) |
|
|
研制成本与搭载费用之和(万元/件) |
20 |
30 |
计划最大资金额300万元 |
|
产品重量(千克/件) |
10 |
5 |
最大搭载重量110千克 |
|
预计收益(万元/件) |
80 |
60 |
|
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
[解析] 设搭载产品Ax件,产品By件,
预计收益z=80x+60y.
则,作出可行域,如图
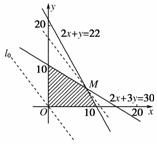
作出直线l0:4x+3y=0并平移,由图象得,当直线经过M点时z能取得最大值,,
解得即M(9,4).
所以zmax=80×9+60×4=960(万元).
[答案] 搭载产品A9件,产品B4件,可使得总预计收益最大,为960万元.
11.(15分)设S为平面上以A(3,-1),B(-1,1),C(1,3)为顶点的三角形区域(含三角形内部及边界).若点(x,y)在区域S上变动.
(1)求z=3x-2y的最值;
(2)求z=y-x的最大值,并指出其最优解;
(3)若x,y为整数,求z=y-x的最大值,并指出其最优解.
[解析] (1)z=3x-2y可化为y=x-=x+b,
故求z的最大值、最小值,相当于求直线y=x+b在y轴上的截距b的最小值、最大值.即b取最大值时,z取最小值;反之亦然.
如图(1)所示,直线y=x左、右平行移动,
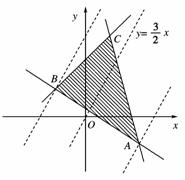
(1)
当y=x+b过B点时,bmax=,此时zmin=-2b=-5;
当y=x+b过A点时,
bmin=-,此时
zmax=-2b=11.
(2)z=y-x可化为y=x+z,故求z的最大值,相当于求直线y=x+z在y轴上的截距z的最大值.如图(2)所示,直线y=x平行移动,
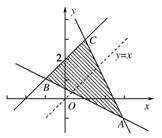
当直线y=x+z与直线BC重合时,zmax=2,此时线段BC上任一点的坐标都是最优解.
(3)由(2)可知zmax=2,最优解都在线段BC上,且x,y为整数,所以最优解有(-1,1),(0,2),(1,3).
10.(15分)某班计划用少于100元的钱购买单价分别为2元和1元的大小彩球装点联欢晚会的会场,根据需要,大球数不少于10个,小球数不少于20个,请你给出几种不同的购买方案?
[解析] 设可购买大球x个,小球y个.
依题意有其整数解为,,,,…都符合题目要求(满足2x+y-100<0即可).
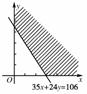
9.某实验室需购某种化工原料106千克,现在市场上有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元,在满足需要的条件下,最少要花费________元.
[解析] 设购买第一种包装x袋,第二种包装y袋,由已知条件35x+24y≥106,x≥0,y≥0,
则当x=1,y=3时,z=140x+120y,取到最小值500元.
[答案] 500
8.若实数x,y满足,z=3x+2y,则z的取值范围是______.
[解析] 作出图象可知,此平面区域是以O(0,0),A(0,1),B为顶点的三角形内部(包括边界),当x=0,y=0时,x+2y取得最小值0;当x=0,y=1时,x+2y取得最大值2.又因为指数函数y=3x在[0,2]上为增函数,故z=3x+2y的取值范围为[1,9].
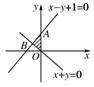
[答案] [1,9]
7.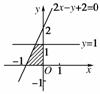 能表示图中阴影部分的二元一次不等式组是________.
能表示图中阴影部分的二元一次不等式组是________.
[解析] 由阴影部分知
x≤0,0≤y≤1,
又2×0-0+2>0,
故2x-y+2≥0,
∴所求二元一次不等式组为.
[答案]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com