2．(2008年广东卷)经过圆x²+2x+y²＝0的圆心C，且与直线x+y＝0垂直的直线方程是

(　)

A．x－y+1＝0　 　　　　　　　　　　　　　　　 B．x－y－1＝0

C．x+y－1＝0　 　　　　　　　　　　　　　　　 D．x+y+1＝0

[解析]　圆x²+2x+y²＝0的圆心(－1,0)且与直线x+y＝0垂直．

所求直线的斜率k＝1，所求直线方程y＝1(x+1)，

∴y＝x+1.故选A.

[答案]　A

1．两条直线y＝x+2a，y＝2x+a的交点P在圆(x－1)²+(y－1)²＝4的内部，则实数a的取值范围是

(　)

A．－＜a＜1　　　　　B．a＞1或a＜－

C．－≤a＜1　 　　　　　　　　　　　　 　D．a≥1或a≤－

[解析]　由，得P(a,3a)，

∴(a－1)²+(3a－1)²＜4，

∴－＜a＜1.

[答案]　A

12．(16分)已知点P是圆x²+y²＝4上一个动点，定点Q的坐标为(4,0)．

(1)求线段PQ的中点的轨迹方程；

(2)设∠POQ的平分线交PQ于点R(O为原点)，求点R的轨迹方程．

[解析]　(1)设线段PQ的中点坐标为M(x，y)，由Q(4,0)可得点P(2x－4,2y)，代入圆的方程x²+y²＝4可得(2x－4)²+(2y)²＝4，整理可得所求轨迹方程为(x－2)²+y²＝1.

(2)设点R(x，y)，P(m，n)，由已知|OP|＝2，|OQ|＝4，

∴＝，由角平分线性质可得＝＝.

又∵点R在线段PQ上，∴＝，∴点R分有向线段的比为，由定比分点坐标公式可得

即

∴点P的坐标为，代入圆的方程x²+y²＝4可得²+²＝4，即²+y²＝(y≠0)．

∴点R的轨迹方程为²+y²＝(y≠0)．

11．(15分)设F(m,0)(m>0)为定点，P，M，N为动点，且P，M分别在y轴和x轴上，若·＝0，+＝0，求点N的轨迹C的方程．

[解析]　设N(x，y)，M(x_0,0)，P(0，y₀)，

则＝(x₀，－y₀)，＝(m，－y₀)，＝(x，y－y₀)，

由·＝0，得mx₀+y＝0，

由+＝0，得(x₀+x，y－2y₀)＝0，

∴将代入mx₀+y＝0，得y²＝4mx即为所求．

10．(15分)已知⊙C：(x+1)²+(y－3)²＝4，由动点P向⊙C引两条切线PA、PB，A、B为切点，使∠APB始终保持60°，求动点P的轨迹方程．

[解析]　由已知在Rt△CAP中，∠CAP＝90°，∠APC＝30°

|CA|＝2，则|PC|＝4，∴P点轨迹是以C(－1,3)为圆心，4为半径的圆．

故动点P的轨迹方程为(x+1)²+(y－3)²＝16.

9．曲线C₁的方程为f(x，y)＝0，曲线C₂的方程为φ(x，y)＝0，点M的坐标为(a，b)，命题p：M∉C₁∩C₂；命题q：，则p是q的________条件．

[解析]　由q：M∉C₁且M∉C₂，∴M∉C₁∩C₂，p成立．

由p：可能有M∈C₁但M∉C₂或M∈C₂但M∉C₁，q不一定成立．

∴p是q的必要非充分条件．

[答案]　必要非充分

8．如图，已知点A、B分别在x、y轴的正半轴上运动，且|AB|＝2a(a＞0)，则AB的中点M的轨迹方程是________．

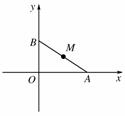
[解析]　设M(x，y)，由中点坐标公式得A(2x,0)，B(0,2y)，

∴＝2a，化简得x²+y²＝a².

∵点A、B分别在x、y轴的正半轴上，∴点M在第一象限，

即x＞0，y＞0，故点M的轨迹方程为：x²+y²＝a²(x＞0，且y＞0)．

[答案]　x²+y²＝a²(x＞0且y＞0)

7．已知△ABC的顶点B(0,0)，C(5,0)，AB边上的中线长|CD|＝3，则顶点A的轨迹方程是____________．

[解析]　设A点坐标为(x，y)，则D.

∴|CD|＝＝3(y≠0)．

整理得(x－10)²+y²＝36(y≠0)

[答案]　(x－10)²+y²＝36(y≠0)

6．平面直角坐标系中，O为坐标原点，已知两点A(3,1)，B(－1,3)，若点C满足＝α+β，其中α、β∈R且α+β＝1，则点C的轨迹方程为

(　)

A．3x+2y－11＝0　 　　　　　　　　　 B．(x－1)²+(y－2)²＝5

C．2x－y＝0　 　　　　　　　　　　　　　 D．x+2y－5＝0

[解析]　设C(x，y)，则(x，y)＝α(3,1)+β(－1,3)

＝(3α－β，α+3β)，则

解得.

代入α+β＝1，得x+2y－5＝0.故选D.

[答案]　D

5．若直线y＝kx+1与曲线x²+y²+kx－y＝0的两个交点恰好关于y轴对称，则k等于

(　)

A．0　 　　　　　　　　　　　　　　　 B．1

C．2　 　　　　　　　　　　　　　　　 D．3

[解析]　由消去y得

(1+k²)x²+2kx＝0，

∴x₁＝0，x₂＝－.

∵两个交点关于y轴对称，

∴x₁＝－x₂，∴k＝0.

[答案]　A