12．(16分)已知圆满足①截y轴所得的弦长为2；②被x轴分成两段圆弧，其弧长的比为3∶1；③圆心到直线l：x－2y＝0的距离为.求该圆的方程．

[解析]　设所求圆心为P(a，b)，半径为r，

则圆心到x轴，y轴的距离分别为|b|、|a|，

因圆P截y轴得弦长为2，

由勾股定理得r²＝a²+1，

又圆被x轴分成两段圆弧弧长的比为3∶1，

∴劣弧所对圆心角90°，

故r＝b，即r²＝2b²

∴2b²－a²＝1①

又∵P(a，b)到直线x－2y＝0的距离为，

得＝，

即a－2b＝±1.②

解①②组成的方程组得或

于是r²＝2b²＝2，

所以，所求圆的方程为(x+1)²+(y+1)²＝2或(x－1)²+(y－1)²＝2.

11．(15分)已知以点C(t∈R，t≠0)为圆心的圆与x轴交于点O、A，与y轴交于点O、B，其中O为原点．

(1)求证：△OAB的面积为定值；

(2)设直线y＝－2x+4与圆C交于点M，N，若OM＝ON，求圆C的方程．

[解析]　(1)证明：设圆的方程为x²+y²+Dx+Ey＝0，

由于圆心C，

∴D＝－2t，E＝－，

令y＝0得x＝0或x＝－D＝2t，

∴A(2t,0)，

令x＝0得y＝0或y＝－E＝，∴B，

∴S_△OAB＝|OA|·|OB|＝·|2t|·

＝4(定值)

(2)∵OM＝ON，

∴O在MN的垂直平分线上，

而MN的垂直平分线过圆心C，

∴k_OC＝，

∴＝，解得t＝2或t＝－2，

而当t＝－2时，直线与圆C不相交，∴t＝2，

∴D＝－4，E＝－2，

∴圆的方程为x²+y²－4x－2y＝0.

10．(15分)根据下列条件，求圆的方程：

(1)经过A(6,5)、B(0,1)两点，并且圆心在直线3x+10y+9＝0上；

(2)经过P(－2,4)、Q(3，－1)两点，并且在x轴上截得的弦长等于6.

[解析]　(1)∵AB的中垂线方程为3x+2y－15＝0，

由解得

∴圆心为C(7，－3)．

又|CB|＝，

故所求圆的方程为(x－7)²+(y+3)²＝65.

(2)设圆的方程为x²+y²+Dx+Ey+F＝0，将P、Q点的坐标分别代入得

又令y＝0，得x²+Dx+F＝0　　　　　　　③

由|x₁－x₂|＝6有D²－4F＝36.　 　　　　　　　　　　　　　　　　　　　　　　　 ④

由①②④解得D＝－2，E＝－4，F＝－8

或D＝－6，E＝－8，F＝0.

故所求圆的方程为x²+y²－2x－4y－8＝0，

或x²+y²－6x－8y＝0.

9．圆心在原点且圆周被直线3x+4y+15＝0分成1∶2两部分的圆的方程为________________．

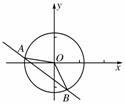
[解析]　如图，因为圆周被直线3x+4y+15＝0分成1∶2两部分，所以∠AOB＝120°.而圆心到直线3x+4y+15＝0的距离d＝＝3，在△AOB中，可求得OA＝6.所以所求圆的方程为x²+y²＝36.

[答案]　x²+y²＝36

8．圆心在直线2x－y－7＝0上的圆C与y轴交于两点A(0，－4)，B(0，－2)，则圆C的方程为______________．

[解析]　∵AB的中垂线y＝－3必过圆心，故解得圆心坐标为C(2，－3)，|CA|＝，

∴所求圆C的方程为(x－2)²+(y+3)²＝5.

[答案]　(x－2)²+(y+3)²＝5

7．圆(x－2)²+y²＝4上到直线y＝x的距离等于2－的点有________个．

[解析]　圆心到直线的距离d＝＝，

半径r＝2.

结合图形可得，共有3个这样的点．

[答案]　3

6．(2008年山东卷)已知圆的方程为x²+y²－6x－8y＝0.设该圆过点(3,5)的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积为

(　)

A．10 　　　 　　　　　　　　　　　　　 B．20

C．30　 　　　　　　　　　　　　　　　　 D．40

[解析]　圆的标准方程为(x－3)²+(y－4)²＝5²，

由题意得|AC|＝2×5＝10，|BD|＝2·＝4，

且AC⊥BD，四边形ABCD的面积S＝|AC|·|BD|＝×10×4＝20.故选B.

[答案]　B

5．已知圆x²+y²+2x－4y+1＝0关于直线2ax－by+2＝0(a，b∈R)对称，则ab的取值范围是

(　)

A.　 　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　 D.

[解析]　将圆的方程配方得：(x+1)²+(y－2)²＝4，若圆关于已知直线对称，即圆心在直线上代入整理得：a+b＝1，故ab＝a(1－a)＝－²+≤，故选A.

[答案]　A

4．若a≠0，则方程x²+y²+ax－ay＝0所表示的图形

(　)

A．关于x轴对称　 　　　　　　　　　　　　　　 B．关于y轴对称

C．关于直线x－y＝0对称　 　　　　　　　 D．关于直线x+y＝0对称

[解析]　x²+y²+ax－ay＝0表示圆，圆心为(－，)，在直线x+y＝0上．

[答案]　D

3．当a为任意实数时，直线(a－1)x－y+a+1＝0恒过点C，则以C为圆心，半径为的圆的方程为

(　)

A．x²+y²－2x+4y＝0　 　　　　　　　　　 B．x²+y²+2x+4y＝0

C．x²+y²+2x－4y＝0　 　　　　　　　　　 D．x²+y²－2x－4y＝0

[解析]　将已知直线化为y－2＝(a－1)(x+1)，可知直线恒过定点(－1,2)，故所求圆的方程为x²+y²+2x－4y＝0.

[答案]　C