
21.(本小题满分15分)已知函数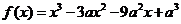 .
.
(1)设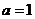 ,求函数
,求函数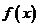 的极值;
的极值;
(2)若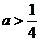 ,且当
,且当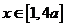 时,
时,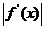
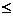 12a恒成立,试确定
12a恒成立,试确定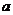 的取值范围.
的取值范围.
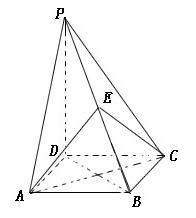
20.(本小题满分14分)如图,四棱锥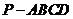 的底面是正方形,
的底面是正方形,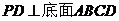 ,点
,点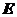 在棱
在棱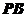 上.
上.
(Ⅰ)求证:平面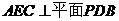 ;
;
(Ⅱ)当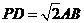 且
且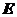 为
为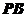 的中点时,求
的中点时,求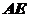 与平面
与平面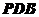 所成的角的大小.
所成的角的大小.
19.(本小题满分14分)设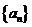 为等比数列,且其满足:
为等比数列,且其满足: .
.
(1)求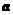 的值及数列
的值及数列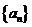 的通项公式;
的通项公式;
(2)数列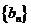 的通项公式为
的通项公式为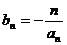 ,求数列
,求数列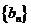 的前n项和
的前n项和 .
.
18.(本小题满分14分)设锐角三角形ABC的内角A,B,C的对边长分别为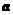 ,b ,c
,
,b ,c
,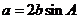 .
.
(1)求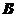 的大小;
的大小;
(2)若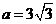 ,
,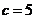 ,求b .
,求b .
17.在平面几何里,有:“若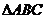 的三边长分别为
的三边长分别为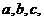 内切圆半径为
内切圆半径为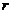 ,则三角形面积为
,则三角形面积为 ”,拓展到空间,类比上述结论,“若四面体
”,拓展到空间,类比上述结论,“若四面体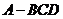 的四个面的面积分别为
的四个面的面积分别为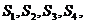 内切球的半径为
内切球的半径为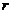 ,则四面体的体积为
”
,则四面体的体积为
”
16.某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等.若一月至十月份销售总额至少达7000万元,则x的最小值是 .
15.已知集合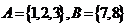 ,现从A,
B中各取一个数字, 组成无重复数字的二位数, 在这些二位数中, 任取一个数,
则恰为奇数的概率为
,现从A,
B中各取一个数字, 组成无重复数字的二位数, 在这些二位数中, 任取一个数,
则恰为奇数的概率为
14.已知1,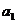 ,
,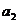 ,9成等差数列,1,
,9成等差数列,1,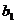 ,
,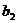 ,
,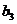 ,9成等比数列,且
,9成等比数列,且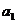 ,
,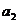 ,
,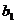 ,
,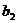 ,
,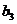 都是实数,则
都是实数,则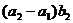 =
.
=
.
13.已知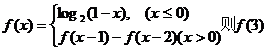 = .
= .
12.若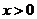 ,则
,则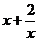 的最小值为
。
的最小值为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com