
4.(2009年郑州模拟)已知函数f(n)=cos (n∈N),则的值为( )
A.1 B.cos
C. D.2
[解析] 函数f(n)的周期为10,
且f(1)+f(2)+f(3)+…+f(10)=0,
∴f(1)+f(2)+f(3)+…+f(2 003)
=f(1)+f(2)+f(3)=cos +cos +cos ,
又f(11)+f(22)+f(33)=cos +cos +cos =cos +cos +cos ,
∴原式=1.
[答案] A
3.函数f(x)=tan ωx(ω>0)图象的相邻的两支截直线y=所得线段长为,则f的值是( )
A.0 B.1
C.-1 D.
[解析] 由题意知T=,由=得ω=4,
∴f(x)=tan 4x,∴f=tan π=0.
[答案] A
2.(2009年石家庄模拟)已知在函数f(x)=sin 图象上,相邻的一个最大值点与一个最小值点恰好在x2+y2=R2上,则f(x)的最小正周期为( )
A.1 B.2
C.3 D.4
[解析] ∵x2+y2=R2,∴x∈[-R,R].
∵函数f(x)的最小正周期为2R,
∴最大值点为
相邻的最小值点为,
代入圆方程,得R=2,∴T=4.
[答案] D
1.函数y=,x∈(-π,0)∪(0,π)的图象可能是下列图象中的( )
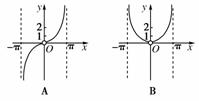
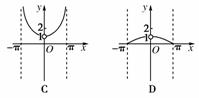
[解析] ∵y=是偶函数,排除A,
当x=2时,y=>2,排除D,
当x=时,y==>1,排除B.
[答案] C
12.已知函数f(x)=sin2x+sinxcosx+2cos2x,x∈R.
(1)求函数f(x)的最小正周期;
(2)将函数f(x)的图象按向量a=(,-)平移后得到函数g(x)的图象,求g(x)的解析式;
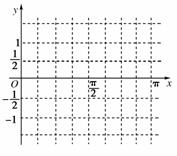
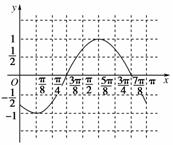
(3)画出函数y=g(x)在区间[0,π]上的图象.
[解析] (1)f(x)=+sin2x+(1+cos2x)
=sin 2x+cos 2x+
=sin (2x+)+
∴f(x)的最小正周期T==π.
(2)把f(x)图象上所有的点按向量a=(,-)平移后,所得到的图象的解析式为
g(x)=sin[2(x-)+]+-=sin(2x-).
(3)由y=sin(2x-)知
|
x |
0 |
|
|
|
|
π |
|
y |
- |
-1 |
0 |
1 |
0 |
- |
故函数y=g(x)在区间[0,π]上的图象如图.
11.据市场调查,某种商品一年内每件出厂价在6千元的基础上,按月呈f(x)=Asin(ωx+φ)+B的模型波动(x为月份),已知3月份达到最高价8千元,7月份价格最低为4千元;该商品每件的售价为g(x)(x为月份),且满足g(x)=f(x-2)+2.
(1)分别写出该商品每件的出厂价函数f(x)、售价函数g(x)的解析式;
(2)问哪几个月能盈利?
[解析] (1)f(x)=Asin(ωx+φ)+B,由题意可得A=2,B=6,ω=,φ=-,
所以f(x)=2sin+6(1≤x≤12,x为正整数),
g(x)=2sin+8(1≤x≤12,x为正整数).
(2)由g(x)>f(x),得sinx<.
2kπ+π<x<2kπ+π,k∈Z,
∴8k+3<x<8k+9,k∈Z,
∵1≤x≤12,k∈Z,∴k=0时,3<x<9,
∴x=4,5,6,7,8;
k=1时,11<x<17,∴x=12.
∴x=4,5,6,7,8,12
答:其中4,5,6,7,8,12月份能盈利.
10.已知电流i与时间t的函数关系式为i=Asin(ωt+φ).
(1)如图是i=Asin(ωt+φ)(ω>0,|φ|<)在一个周期内的图象,根据图中数据求i=Asin(ωt+φ)的解析式.
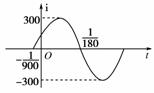
(2)如果t在任意一段秒时间内,电流i=Asin(ωt+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?
[解析] (1)由题图可知,A=300,
周期T=2(+)=,所以ω==150π.
又当t=时,i=0,即sin(150π·+φ)=0,
又∵|φ|<,∴φ=.
故所求函数的解析式为i=300sin(150πt+).
(2)依题意,周期T≤,即≤(ω>0),
∴ω≥300π>942,又ω∈N*,
所以ω的最小正整数值为943.
9.(2008年辽宁高考)已知f(x)=sin(ω>0),f=f,且f(x)在区间上有最小值,无最大值.则ω________.
[解析] ∵f=f且f(x)在上
只有最小值而无最大值.
∴f(x)在x=时取最小值,
且f(x)的周期T>.
∴
∴
∴当k=1时,ω=.
[答案]
8.设函数y=cosx的图象位于y轴右侧的所有的对称中心从左依次为A1,A2,…,An,…,则A50的坐标是________.
[解析] 由x=+kπ得x=2k+1(k∈Z),即对称中心横坐标为x=2k+1,k≥0且k∈N,
当k=49时,x=99,
则A50的坐标为(99,0).
[答案] (99,0)
7.定义行列式运算\o(\s\up7(a1a3=a1a4-a2a3.将函数f(x)=\o(\s\up7(\r(31的图象向左平移n(n>0)个单位,所得图象对应的函数为偶函数,则n的最小值为________.
[解析] f(x)=\o(\s\up7(\r(31=cosx-sinx
=2cos,图象向左平移n(n>0)个单位,
得f(x+n)=2cos,则当n取得最小值π时,函数为偶函数.
[答案] π
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com