12.

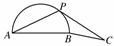
如图，点P在以AB为直径的半圆上移动，且AB＝1，过点P作圆的切线PC，使PC＝1.连BC，当点P在什么位置时，四边形ABCP的面积等于？

[解析]　设∠PAB＝α，连接PB.

∵AB是直径，∴∠APB＝90°.

又AB＝1，∴PA＝cos α，PB＝sin α.

∵PC是切线，∴∠BPC＝α.又PC＝1，

∴S_{四边形ABCP}＝S_△APB+S_△BPC

＝PA·PB+PB·PC·sin α

＝cos αsin α+sin² α

＝sin 2α+(1－cos 2α)

＝(sin 2α－cos 2α)+

＝sin+.

由已知，sin+＝，

∴sin＝.

又α∈，∴2α－∈.

∴2α－＝，∴α＝.

故当点P位于AB的中垂线与半圆的交点时，四边形ABCP的面积等于.

11．(2008年北京高考)已知函数f(x)＝sin² ωx+sin ωx·sin(ωx+)(ω>0)的最小正周期为π.

(1)求ω的值；

(2)求函数f(x)在区间上的取值范围．

[解析]　(1)f(x)＝+sin 2ωx

＝sin 2ωx－cos 2ωx+

＝sin+.

因为函数f(x)的最小正周期为π，且ω>0.

所以＝π，解得ω＝1.

(2)由(1)得f(x)＝sin+.

∵0≤x≤π，

∴－≤2x－≤π，

∴－≤sin≤1，

∴0≤sin+≤，

即f(x)的取值范围为.

10．已知f(x)＝+，且x≠2kπ+，k∈Z.

(1)化简f(x)；

(2)是否存在x，使tan·f(x)与相等？若存在，求出x；若不存在，说明理由．

[解析]　(1)f(x)＝+

＝+

＝+

＝－－

＝－＝－.

(2)假设存在x使得tan·f(x)与相等，

则tan·＝，

∴－2tan＝1+tan²，

即(tan+1)²＝0，∴tan＝－1，

∴＝－+kπ，k∈Z，

即x＝－+2kπ，k∈Z，

故存在x＝－+2kπ(k∈Z)使tan·f(x)与相等．

9．(2009年上海模拟)函数f(x)＝2²+sin x的最小正周期是________．

[解析]　∵f(x)＝2²+sin x＝1+cos x+sin x

＝sin+1.

∴f(x)的最小正周期为2π.

[答案]　2π

8．设α是第二象限的角，tan α＝－，且sin<cos，则cos＝________.

[解析]　∵α是第二象限的角，

∴可能在第一或第三象限，

又sin<cos∴为第三象限的角，

∴cos<0.∵tan α＝－，

∴cos α＝－，∴cos＝－＝－

[答案]　－

7．若＝3，tan(β－α)＝－2，则tan(β－2α)＝________.

[解析]　∵＝＝3，∴tan α＝2.

又tan(β－α)＝－2，

∴tan(β－2α)＝tan

＝＝＝.

[答案]　

6．(2009年惠安模拟)若sin＝，则cos＝(　)

A．－　 　　　　　　　　　　　　　　　　　　　　 B．－

C.　 　　　　　　　　　　　　　　　　　　　　　　　　 D.

[解析]　∵sin＝，

∴cos＝cos

＝1－2sin²

＝1－2ײ＝，

∴cos＝cos

＝－cos＝－.

[答案]　B

5．(2009年汤阴模拟)若2^a＝sin 2+cos 2，则实数a的值所在范围是(　)

A.　 　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　 D.

[解析]　sin 2+cos 2＝2sin

≈2sin 144.6°＝2sin 35.4°.

∵sin 30°<sin 35.4°<sin 45°，

∴<sin 35.4°<，

∴1<sin 2+cos 2<，

即1<2^a<，∴0<a<.

[答案]　A

4．(2008年广东四校联考)已知0<α<π，3sin 2α＝sin α，则cos(α－π)等于(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　 B．－

C.　 　　　　　　　　　　　　　　　　　　　　　　　　 D．－

[解析]　∵0<α<π，3sin 2α＝sin α，

∴6sin αcos α＝sin α，又∵sin α≠0，∴cos α＝，

cos(α－π)＝cos(π－α)＝－cos α＝－.

[答案]　D

3．(2009年大同模拟)函数f(x)＝sin²(x+)－sin²(x－)是(　)

A．周期为2π的奇函数

B．周期为2π的偶函数

C．周期为π的奇函数

D．周期为π的偶函数

[解析]　f(x)＝sin²－sin²

＝－

＝cos－cos

＝sin 2x+sin 2x＝sin 2x，

∴f(x)是周期为π的奇函数．

[答案]　C