
15. 解:(Ⅰ)y=5x2+ (100-x)2(10≤x≤90);………………………………………5分
(100-x)2(10≤x≤90);………………………………………5分
(Ⅱ)由y=5x2+ (100-x)2=
(100-x)2= x2-500x+25000=
x2-500x+25000=
 +
+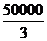 .
.
则当x=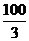 米时,y最小. 故当核电站建在距A城
米时,y最小. 故当核电站建在距A城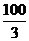 米时,才能使供电费用最小.
米时,才能使供电费用最小.
14、解:⑴由题义得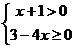 解方程组的
解方程组的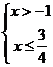 即得函数的定义域为
即得函数的定义域为
⑵任给 有
有 
∵

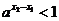 ∴
∴
即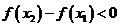 ∴函数
∴函数 在
在 上是减函数. ………6分
上是减函数. ………6分
10、 ; 11、 ②③
; 12、2 ; 13、
; 11、 ②③
; 12、2 ; 13、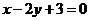 ;
;
1、  ; 2 、(4); 3、 2 ; 4、-1;5、
; 2 、(4); 3、 2 ; 4、-1;5、 ;6、3:1:2;7、
;6、3:1:2;7、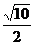 ;8、
;8、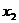 <
<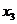 <
<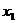
18、函数 ,当
,当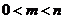 时,有
时,有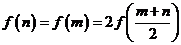 .
.
⑴求 的值;
的值;
⑵求证:
高一新课程质量检测上学期测试数学试题08.1.29
17、 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
 (1) FD∥平面ABC;
(1) FD∥平面ABC;
(2) AF⊥平面EDB.
16、对于函数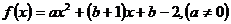 ,若存在实数
,若存在实数 ,使
,使 =
= 成立,则
成立,则
称 为
为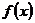 的不动点.
的不动点.
⑴当 时,求
时,求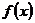 的不动点;
的不动点;
⑵若对于任意实数 ,函数
,函数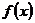 恒有两个不相同的不动点,求
恒有两个不相同的不动点,求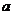 的取值范围.
的取值范围.
15、⑴已知△ABC三个顶点的坐标分别为A(4,1),B(0,3),C(2,4),边AC的中
点为D,求AC边上中线BD所在的直线方程并化为一般式;
⑵已知圆C的圆心是直线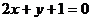 和
和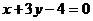 的交点上且与直线
的交点上且与直线
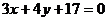 相切,求圆C的方程.
相切,求圆C的方程.
14、A、B两城相距100km,在两地之间距A城xkm处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数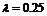 .若A城供电量为20亿度/月,B城为10亿度/月.
.若A城供电量为20亿度/月,B城为10亿度/月.
(Ⅰ)把月供电总费用y表示成x的函数,并求定义域;
(Ⅱ)核电站建在距A城多远,才能使供电费用最小.
12、已知圆 ,过点
,过点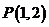 的最短弦所在的直线
的最短弦所在的直线 的方程是
.
的方程是
.
13 按要求完成下列各题:
⑴求函数 的定义域;
的定义域;
⑵当 时,证明函数
时,证明函数 在
在 上是减函数.
上是减函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com