
24.(2010年浙江省东阳市)(6分)如图,已知BE⊥AD,CF⊥AD,且BE=CF.
(1)
 请你判断AD是△ABC的中线还是角平分线?请证明
请你判断AD是△ABC的中线还是角平分线?请证明
你的结论.
(2)连接BF、CE,若四边形BFCE是菱形,则△ABC中应
添加一个条件 ▲
[关键词]三角形的全等
[答案](1)AD是△ABC的中线.................................1分
理由如下:∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°.........1分
又∵BE=CF,∠BDE=∠CFD ∴△BDE≌△CFD(AAS).......2分
(2)AB=AC或∠ABC=∠ACB或AD⊥BC或AD平分∠BAC.......2分
23.(2010年四川省眉山市)如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
[关键词]平行四边形的判定、菱形的性质与判定和面积、矩形的性质
 [答案]解:(1)四边形OCED是菱形.
[答案]解:(1)四边形OCED是菱形.
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
又 在矩形ABCD中,OC=OD,
∴四边形OCED是菱形.
(2)连结OE.由菱形OCED得:CD⊥OE,
∴OE∥BC
又 CE∥BD
∴四边形BCEO是平行四边形
∴OE=BC=8
∴S四边形OCED=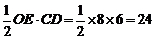
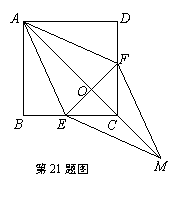
22.(2010年宁德市)(本题满分13分)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
⑴ 求证:△AMB≌△ENB;
⑵ ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
 ⑶
当AM+BM+CM的最小值为
⑶
当AM+BM+CM的最小值为 时,求正方形的边长.
时,求正方形的边长.
[答案]解:⑴∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN-∠ABN=∠ABE-∠ABN.
即∠BMA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS).
⑵①当M点落在BD的中点时,AM+CM的值最小.
 ②如图,连接CE,当M点位于BD与CE的交点处时,
②如图,连接CE,当M点位于BD与CE的交点处时,
AM+BM+CM的值最小. ………………9分
理由如下:连接MN.由⑴知,△AMB≌△ENB,
∴AM=EN.
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
⑶过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=90°-60°=30°.
设正方形的边长为x,则BF=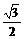 x,EF=
x,EF= .
.
在Rt△EFC中,
∵EF2+FC2=EC2,
∴( )2+(
)2+(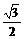 x+x)2=
x+x)2= .
.
解得,x=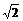 (舍去负值).
(舍去负值).
∴正方形的边长为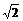 .
.
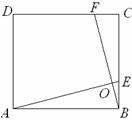
21. (2010年浙江省绍兴市) (1) 如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.
求证:BE=CF.
|
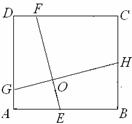 (2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,
(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,
BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF
=4.求GH的长.
(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,
∠FOH=90°,EF=4. 直接写出下列两题的答案:
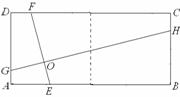
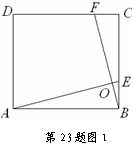
①如图3,矩形ABCD由2个全等的正方形组成,求GH的长;
②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).
|
|||
|
|||

[答案](1) 证明:如图1,∵ 四边形ABCD为正方形,
∴ AB=BC,∠ABC=∠BCD=90°,
∴ ∠EAB+∠AEB=90°.
∵ ∠EOB=∠AOF=90°,
∴ ∠FBC+∠AEB=90°,∴ ∠EAB=∠FBC,
∴ △ABE≌△BCF , ∴ BE=CF.
 (2) 解:如图2,过点A作AM//GH交BC于M,
(2) 解:如图2,过点A作AM//GH交BC于M,
过点B作BN//EF交CD于N,AM与BN交于点O/,
则四边形AMHG和四边形BNFE均为平行四边形,
∴ EF=BN,GH=AM,
∵ ∠FOH=90°, AM//GH,EF//BN, ∴ ∠NO/A=90°,
故由(1)得, △ABM≌△BCN, ∴ AM=BN,
∴ GH=EF=4.
(3) ① 8.② 4n.
20.(2010年四川省眉山)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(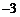 ,0)、(0,4),抛物线
,0)、(0,4),抛物线 经过B点,且顶点在直线
经过B点,且顶点在直线 上.
上.
(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
 (3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
[关键词]抛物线、菱形、最值
[答案] 解:(1)由题意,
可设所求抛物线对应的函数关系式为 …(1分)
…(1分)
∴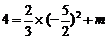
∴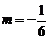 ……………………………………………………………(3分)
……………………………………………………………(3分)
∴所求函数关系式为: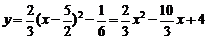 …………(4分)
…………(4分)
(2)在Rt△ABO中,OA=3,OB=4,
∴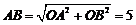
∵四边形ABCD是菱形
∴BC=CD=DA=AB=5 ……………………………………(5分)
∴C、D两点的坐标分别是(5,4)、(2,0). …………(6分)
当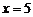 时,
时,
当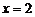 时,
时,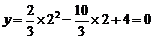
∴点C和点D在所求抛物线上. …………………………(7分)
(3)设直线CD对应的函数关系式为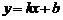 ,则
,则


解得: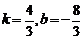 .
.
∴ ………(9分)
………(9分)
∵MN∥y轴,M点的横坐标为t,
∴N点的横坐标也为t.
则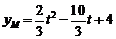 ,
,  ,……………………(10分)
,……………………(10分)
∴
∵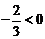 , ∴当
, ∴当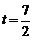 时,
时, ,
,
此时点M的坐标为( ,
,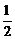 ). ………………………………(12分)
). ………………………………(12分)
18.(2010年山东省青岛市)已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.
(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
[关键词]菱形的判定
[答案]证明:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B = ∠D = 90°.
∵AE = AF,
∴ .
.
∴BE=DF.
 (2)四边形AEMF是菱形.
(2)四边形AEMF是菱形.
∵四边形ABCD是正方形,
∴∠BCA = ∠DCA = 45°,BC = DC.
∵BE=DF,
∴BC-BE = DC-DF. 即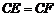 .
.
∴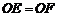 .
.
∵OM = OA,
∴四边形AEMF是平行四边形.
∵AE = AF,
∴平行四边形AEMF是菱形.
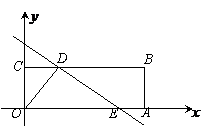
19(.2010年广东省广州市)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线 =-
=- +
+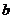 交折线OAB于点E.
交折线OAB于点E.
(1)记△ODE的面积为S,求S与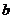 的函数关系式;
的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.

 [关键词]轴对称 四边形 勾股定理
[关键词]轴对称 四边形 勾股定理
[答案](1)由题意得B(3,1).
若直线经过点A(3,0)时,则b=
若直线经过点B(3,1)时,则b=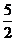
若直线经过点C(0,1)时,则b=1
①
若直线与折线OAB的交点在OA上时,即1<b≤ ,如图25-a,
,如图25-a,


此时E(2b,0)
∴S= OE·CO=
OE·CO= ×2b×1=b
×2b×1=b
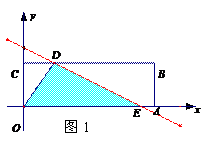
②若直线与折线OAB的交点在BA上时,即 <b<
<b<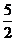 ,如图2
,如图2
此时E(3, ),D(2b-2,1)
),D(2b-2,1)
∴S=S矩-(S△OCD+S△OAE +S△DBE )
= 3-[ (2b-1)×1+
(2b-1)×1+ ×(5-2b)·(
×(5-2b)·( )+
)+ ×3(
×3( )]=
)]=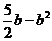
∴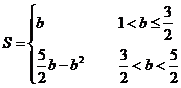
(2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形OA1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积。
本题答案由无锡市天一实验学校金杨建老师草制!
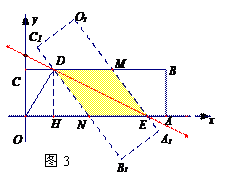

由题意知,DM∥NE,DN∥ME,∴四边形DNEM为平行四边形
根据轴对称知,∠MED=∠NED
又∠MDE=∠NED,∴∠MED=∠MDE,∴MD=ME,∴平行四边形DNEM为菱形.
过点D作DH⊥OA,垂足为H,
由题易知,tan∠DEN=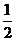 ,DH=1,∴HE=2,
,DH=1,∴HE=2,
设菱形DNEM 的边长为a,
则在Rt△DHM中,由勾股定理知: ,∴
,∴
∴S四边形DNEM=NE·DH=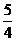
∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为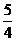 .
.
17.(2010年益阳市)如图7,在菱形ABCD中,∠A=60°,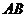 =4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
(1) 求∠ABD 的度数;
(2)求线段 的长.
的长.
[关键词]菱形性质、等边三角形、
[答案]解:⑴ 在菱形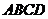 中,
中, ,
,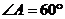
 ∴
∴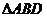 为等边三角形
为等边三角形
∴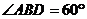
⑵由(1)可知
又∵ 为
为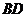 的中点
的中点
∴
又∵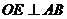 ,及
,及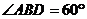
∴
∴
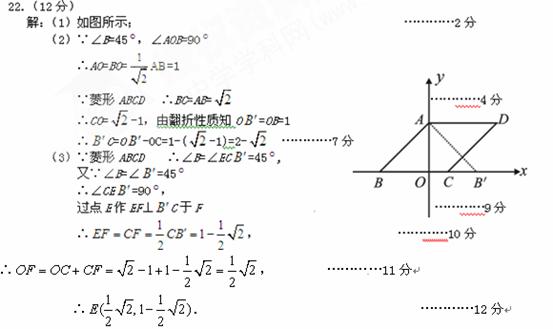
16.(2010福建龙岩中考)22.(12分)
 如图,将边长为
如图,将边长为 的菱形ABCD纸片放置在平面直角坐标
的菱形ABCD纸片放置在平面直角坐标
系中.已知∠B=45°.
(1)画出边AB沿y轴对折后的对应线段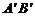 ,
,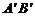
与边CD交于点E;
(2)求 出线段
出线段 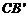 的长;
的长;
(3)求点E的坐标.
15.(2010福建龙岩中考)20.(10分)
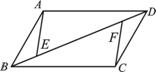 如图,平行四边形ABCD中,E、F是对角线BD上的点,且BE=DF.
如图,平行四边形ABCD中,E、F是对角线BD上的点,且BE=DF.
(1) 请你写出图中所有的全等三角形
请你写出图中所有的全等三角形
(2)试在上述各对全等三角形中找出一对加以证明.

14. (2010年青岛)已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.
(1)求证:BE = DF;
 (2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
[答案]证明:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B = ∠D = 90°.
∵AE = AF,
∴ .
.
∴BE=DF.
(2)四边形AEMF是菱形.
∵四边形ABCD是正方形,
∴∠BCA = ∠DCA = 45°,BC = DC.
∵BE=DF,
∴BC-BE = DC-DF. 即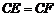 .
.
∴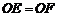 .
.
∵OM = OA,
∴四边形AEMF是平行四边形.
∵AE = AF,
∴平行四边形AEMF是菱形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com