2、已知直线的极坐标方程为，曲线C的参数方程为，设点是曲线C上的任意一点，求到直线的距离的最大值．

(总分40分，加试时间30分钟)

答卷前，请考生务必将自己的学校、姓名、考试号等信息填写在答卷密封线内．解答过程应写在答题卷的相应位置上，在其它地方答题无效．

1、已知矩阵=，求的特征值，及对应的特征向量．

20、(本小题16分)

已知函数，为正常数。

⑴若，且，求函数的单调增区间；

⑵若，且对任意，，都有，求的的取值范围。

19、(本小题16分)

已知数列满足：(为常数)，

数列中，。

⑴求；

⑵证明：数列为等差数列；

⑶求证：数列中存在三项构成等比数列时，为有理数。

18、(本小题16分)

已知抛物线的顶点在坐标原点，对称轴为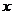轴，焦点在直线上，直线与抛物线相交于两点，为抛物线上一动点(不同于)，直线分别交该抛物线的准线于点。

⑴求抛物线方程；

⑵求证：以为直径的圆经过焦点，且当为抛物线的顶点时，圆与直线相切。

17、(本小题14分)

已知某种稀有矿石的价值(单位：元)与其重量(单位：克)的平方成正比，且克该种矿石的价值为元。

⑴写出(单位：元)关于(单位：克)的函数关系式；

⑵若把一块该种矿石切割成重量比为的两块矿石，求价值损失的百分率；

⑶把一块该种矿石切割成两块矿石时，切割的重量比为多少时，价值损失的百分率最大。

(注：价值损失的百分率；在切割过程中的重量损耗忽略不计)

16、(本小题14分)

已知函数的图像如图所示，

直线是其两条对称轴。

⑴求函数的解析式并写出函数的单调增区间；

⑵若，且，求的值。

15．(本小题14分)

如图，在直三棱柱中，，点在边上，。

⑴求证：平面；

⑵如果点是的中点，求证：平面 .

14．已知等差数列的前n项和为，若，

　，则下列四个命题中真命题的序号为　　 ▲　　 .

①； ②； ③；　 ④

13．在中，，点是内心，且，

则　　 ▲　　 .