
19.(本小题满分13分)
已知中心在原点,焦点在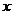 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为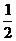 ,且经过点
,且经过点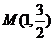 ,过点P(2,1)的直线
,过点P(2,1)的直线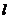 与椭圆C相交于不同的两点A、B.
与椭圆C相交于不同的两点A、B.
(1)求椭圆C的方程;
 (2)是否存直线
(2)是否存直线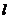 ,满足
,满足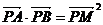 ?
? 若存在,求出直线
若存在,求出直线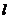 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
18.(本小题满分14分)
已知函数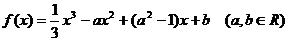 .
.
(Ⅰ)若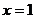 为
为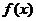 的极值点,求
的极值点,求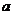 的值;
的值;
(Ⅱ)若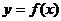 的图象在点(
的图象在点(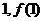 )处的切线方程为
)处的切线方程为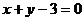 ,求
,求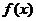 在区间
在区间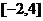 上的最大值;
上的最大值;
(Ⅲ)当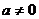 时,若
时,若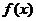 在区间
在区间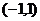 上不单调,求
上不单调,求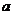 的取值范围.
的取值范围.
17.(本小题满分14分)
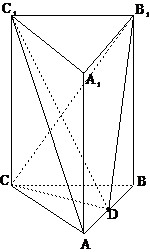 三棱柱
三棱柱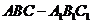 中,
中,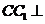 平面
平面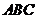 ,
,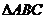 是边长为
是边长为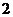 的等边三角形,
的等边三角形,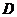 为
为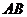 边中点,且
边中点,且 .
.
(Ⅰ)求证:平面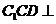 平面
平面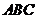 ;
;
(Ⅱ)求证: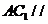 平面
平面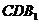 ;
;
(Ⅲ)求三棱 锥
锥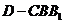 的体积.
的体积.
16.(本小题满分13分)
设函数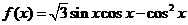 .
.
(Ⅰ)求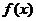 的最小正周期;
的最小正周期;
(Ⅱ)当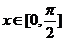 时,求函数
时,求函数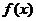 的最大值和最小值.
的最大值和最小值.
15.(本小题满分13分)
已知集合 ,
,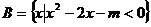 .
.
(1)当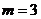 时,求
时,求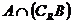 ;(2)若
;(2)若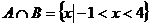 ,求实数
,求实数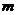 的
的 值.
值.

12. ___________. 13. ; .14. .
9. . 10.____ __. 11. .
14. 定义在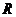 上的偶函数
上的偶函数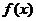 满足
满足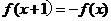 ,且在[-1,0]上是增函数,下面是关于
,且在[-1,0]上是增函数,下面是关于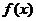 的判断:
的判断:
(1) 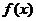 是周期函数;(2)
是周期函数;(2) 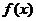 的图像关于直线
的图像关于直线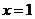 对称;(3)
对称;(3) 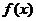 在[0,1]上时增函数;(4)
在[0,1]上时增函数;(4)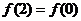 .其中正确命题的序号是
.
.其中正确命题的序号是
.
北京市日坛中学2010-2011学年度第一学期
 摸底考试高三年级数学(文科)答题纸2010.8
摸底考试高三年级数学(文科)答题纸2010.8
命题人:胡芳 复核人:杨秀辉
13. 椭圆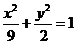 的焦点为
的焦点为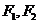 ,点P在椭圆上,若
,点P在椭圆上,若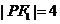 ,则
,则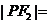 ;
;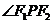 的大小为
.
的大小为
.
12. 设函数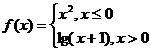 ,若
,若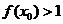 ,则
,则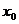 的取值范围为
.
的取值范围为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com