5．在一个塔底的水平面上某点测得该塔顶的仰角为θ，由此点向塔底沿直线行走了30 m，测得塔顶的仰角为2θ，再向塔底前进10 m，又测得塔顶的仰角为4θ，则塔的高度为________．

解析：如图，依题意有PB=BA=30，PC=BC=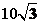.在三角形BPC中，由余弦定理可得

cos2θ=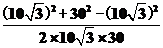

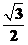=，所以2θ=30°，4θ=60°，在三角形PCD中，

可得PD=PC·sin4θ=10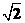·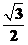=15(m)．

答案：15 m

4.据新华社报道，强台风“珍珠”在广东饶平登陆．台风中心最大风力达到12级以上，大风降雨给灾区带来严重的灾害，不少大树被大风折断．某路边一树干被台风吹断后，折成与地面成45°角，树干也倾斜为与地面成75°角，树干底部与树尖着地处相距20米，则折断点与树干底部的距离是　　　　　　　　　　　　　　　　　　　 (　)

A.米　　　 　B．10米　　　 C.米　 　　　　　D．20米

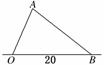解析：如图，设树干底部为O，树尖着地处为B，折断点为A，

则∠ABO=45°，∠AOB=75°，

∴∠OAB=60°.

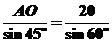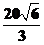由正弦定理知，，∴AO= (米)．

答案：A

3．如图所示，为了测量河对岸A，B两点间的距离，

在这一岸定一基线CD，现已测出CD＝a和∠ACD＝60°，

∠BCD＝30°，∠BDC＝105°，∠ADC＝60°，试求AB的长．

解：在△ACD中，已知CD＝a，∠ACD＝60°，∠ADC＝60°，所以AC＝a.　　 ①

在△BCD中，由正弦定理可得

BC＝＝a.　　　　　　　　　　　　　　　　 　　　　　　　　②

在△ABC中，已经求得AC和BC，又因为∠ACB＝30°，

所以利用余弦定理可以求得A、B两点之间的距离为

AB＝＝a.

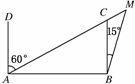
2．一船以每小时15 km的速度向东航行，船在A处看到一灯塔M在北偏东60°方向，行驶4 h后，船到达B处，看到这个灯塔在北偏东15°方向，这时船与灯塔的距离为________km.

解析：如图，依题意有AB＝15×4＝60，∠MAB＝30°，∠AMB＝45°，在△AMB中，由正弦定理得＝，解得BM＝30 km.

答案：30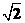

1.一船自西向东航行，上午10时到达灯塔P的南偏西75°、距塔68海里的M处，下午2时到达这座灯塔的东南方向的N处，则这只船航行的速度为　　　　　　　 (　)

A.海里/时　 　　　　　　B．34海里/时

C.海里/时 　　　　　　　D．34海里/时

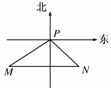解析：如图．由题意知∠MPN=75°+45°=120°，∠PNM=45°.

在△PMN中，由正弦定理，得

，

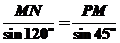∴MN=68×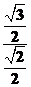=34.

又由M到N所用时间为14-10=4小时，

∴船的航行速度v= 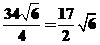(海里/时)．

答案：A

12．(文)(2010·长郡模拟)在△ABC中，内角A，B，C的对边分别为a，b，c，＜C＜且＝

(1)判断△ABC的性状；

(2)若|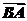+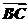|＝2，求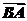·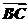的取值范围．

解：(1)由＝及正弦定理得sinB＝sin2C，

∴B＝2C，且B+2C＝π，

若B＝2C，＜C＜，

∴π＜B＜π，B+C＞π(舍)；

∴B+2C＝π，则A＝C，∴△ABC为等腰三角形．

(2)∵|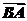+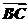|＝2，∴a²+c²+2ac·cosB＝4，

∴cosB＝(∵a＝c)，

而cosB＝－cos2C，＜C＜，

∴＜cosB＜1，

∴1＜a²＜，

又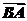·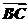＝accosB＝2－a²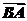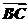，∴·∈(，1)．

(理)(2010·广州模拟)在△ABC中，A，B，C分别是三边a，b，c的对角．设m＝(cos，sin)，n＝(cos，－sin)，m，n的夹角为.

(1)求C的大小；

(2)已知c＝，三角形的面积S＝，求a+b的值．

解：(1)m·n＝cos²－sin²＝cosC，

又m·n＝|m||n|cos＝，

故cosC＝，∵0＜C＜π，∴C＝.

(2)S＝absinC＝absin＝ab，

又已知S＝，故ab＝，∴ab＝6.

∵c²＝a²+b²－2abcosC，c＝，

∴＝a²+b²－2ab×＝(a+b)²－3ab.

∴(a+b)²＝+3ab＝+18＝，

∴a+b＝.

11．已知a，b，c为△ABC的三个内角A，B，C的对边，向量m＝(，－1)，n＝(cosA，sinA)，若m⊥n，且acosB+bcosA＝csinC，则角B＝________.

解析：∵m⊥n，∴cosA－sinA＝0，

∴tanA＝，∴A＝.

∵acosB+bcosA＝csinC，

∴sinAcosB+sinBcosA＝sinCsinC，

∴sin(A+B)＝sin²C，∴sinC＝sin²C，∵sinC≠0，∴sinC＝1.

∴C＝，∴B＝.

答案：

10．(文)在三角形ABC中，已知∠B＝60°，最大边与最小边的比为，则三角形的最大角为　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　(　)

A．60° 　　　　B．75°　　　 C．90°　 　　　　D．115°

解析：不妨设a为最大边．由题意，

＝＝，

即＝，

∴＝，

(3－)sinA＝(3+)cosA，

∴tanA＝2+，∴A＝75°.

答案：B

(理)锐角△ABC中，若A＝2B，则的取值范围是　　　　　　　　　　　　　 (　)

A．(1,2)　 　B．(1，)　　 C．(，2) 　　D．(，)

解析：∵△ABC为锐角三角形，且A＝2B，

∴∴＜B＜，

∴sinA＝sin2B＝2sinBcosB，

＝＝2cosB∈(，)．

答案：D

9.若△ABC的周长等于20，面积是10，A＝60°，则BC边的长是　　　　　 (　)

A．5　　 　B．6 　　　C．7　 　　　D．8

解析：依题意及面积公式S＝bcsinA，

得10＝bcsin60°，得bc＝40.

又周长为20，故a+b+c＝20，b+c＝20－a，

由余弦定理得：a²＝b²+c²－2bccosA＝b²+c²－2bccos60°

＝b²+c²－bc＝(b+c)²－3bc，

故a²＝(20－a)²－120，解得a＝7.

答案：C

8．(2009·浙江高考)在△ABC中，角A，B，C所对的边分别为a，b，c，且满足cos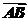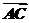＝，·＝3.

(1)求△ABC的面积；

(2)若c＝1，求a的值．

解：(1)因为cos＝，

所以cosA＝2cos²－1＝，sinA＝.

又由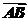·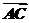＝3，得bccosA＝3，所以bc＝5.

因此S_△ABC＝bcsinA＝2.

(2)由(1)知，bc＝5，又c＝1，所以b＝5，

由余弦定理，得a²＝b²+c²－2bccosA＝20，所以a＝2.