
7.函数y=sin2x-x,x∈[-,]的最大值是________,最小值是________.
解析:∵y′=2cos2x-1=0,∴x=±.
而f(-)=-+,f()=-,
端点f(-)=,f()=-,
所以y的最大值是,最小值是-.
答案: -
6.若函数f(x)=x3-3x+a有3个不同的零点,则实数a的取值范围是 ( )
A.(-2,2) B.[-2,2] C.(-∞,-1) D.(1,+∞)
解析:由f′(x)=3x2-3=3(x-1)(x+1),
且当x<-1时,f′(x)>0;
当-1<x<1时,f′(x)<0;当x>1时,f′(x)>0.
所以当x=-1时函数f(x)有极大值,当x=1时函数f(x)有极小值.
要使函数f(x)有3个不同的零点,只需满足
解之得-2<a<2.
答案:A
5.(文)函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a= ( )
A.2 B.3 C.4 D.5
解析:因为f(x)=x3+ax2+3x-9,所以f′(x)=3x2+2ax+3,由题意有f′(-3)=0,所以3×(-3)2+2a×(-3)+3=0,由此解得a=5.
答案:D
(理)设a∈R,若函数y=ex+ax,x∈R有大于零的极值点,则 ( )
A.a<-1 B.a>-1 C.a>- D.a<-
解析:由y′=(ex+ax)′=ex+a=0得ex=-a,
即x=ln(-a)>0⇒-a>1⇒a<-1.
答案:A
4.设函数f(x)=x3+ax2-9x-1(a<0).若曲线y=f(x)的斜率最小的切线与直线12x+y=6平行,求:
(1)a的值;
(2)函数f(x)的单调区间.
解:(1)因f(x)=x3+ax2-9x-1,
所以f′(x)=3x2+2ax-9
=32-9-.
即当x=-时,f′(x)取得最小值-9-.
因斜率最小的切线与12x+y=6平行,即该切线的斜率为-12,所以-9-=-12,即a2=9.
解得a=±3,由题设a<0,所以a=-3.
(2)由(1)知a=-3,因此f(x)=x3-3x2-9x-1,
f′(x)=3x2-6x-9=3(x-3)(x+1),
令f′(x)=0,解得x1=-1,x2=3.
当x∈(-∞,-1)时,f′(x)>0,
故f(x)在(-∞,-1)上为增函数;
当x∈(-1,3)时,f′(x)<0,
故f(x)在(-1,3)上为减函数;
当x∈(3,+∞)时,f′(x)>0,故f(x)在(3,+∞)上为增函数.
由此可见,函数f(x)的单调递增区间为(-∞,-1)和(3,+∞),单调递减区间为(-1,3).
|
题组二 |
导数与函数的极值和最值 |
3.已知函数y=ax与y=-在(0,+∞)上都是减函数,则函数y=ax3+bx2+5的单调减区间为________.
解析:根据题意a<0,b<0.
由y=ax3+bx2+5,得y′=3ax2+2bx,
令y′<0,可得x>0或x<-,
故所求减区间为(-∞,-)和(0,+∞).
答案:(-∞,-)和(0,+∞)
2.若函数h(x)=2x-+在(1,+∞)上是增函数,则实数k的取值范围是 ( )
A.[-2,+∞) B.[2,+∞) C.(-∞,-2] D.(-∞,2]
解析:因为h′(x)=2+,所以h′(x)=2+=≥0在(1,+∞)上恒成立,即k≥-2x2在(1,+∞)上恒成立,所以k∈[-2,+∞).
答案:A
1.(2009·广东高考)函数f(x)=(x-3)ex的单调递增区间是说明 ( )
A.(-∞,2) B.(0,3) C.(1,4) D.(2,+∞)
解析:f(x)=(x-3)·ex,f′(x)=ex(x-2)>0,
∴x>2.
∴f(x)的单调递增区间为(2,+∞).
答案:D
12.(文)设t≠0,点P(t,0)是函数f(x)=x3+ax与g(x)=bx2+c的图象的一个公共点,两函数的图象在点P处有相同的切线.试用t表示a,b,c.
解:因为函数f(x),g(x)的图象都过点(t,0),
所以f(t)=0,
即t3+at=0.因为t≠0,所以a=-t 2.
g(t)=0,即bt2+c=0,所以c=ab.
又因为f(x),g(x)在点(t,0)处有相同的切线,
所以f′(t)=g′(t).
而f′(x)=3x2+a,g′(x)=2bx,
所以3t2+a=2bt.
将a=-t2代入上式得b=t.因此c=ab=-t3.
故a=-t2,b=t,c=-t3.
(理)已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12,和直线m:y=kx+9,又f′(-1)=0.
(1)求a的值;
(2)是否存在k的值,使直线m既是曲线y=f(x)的切线,又是曲线y=g(x)的切线?如果存在,求出k的值;如果不存在,请说明理由.
解:(1)f′(x)=3ax2+6x-6a,f′(-1)=0,
即3a-6-6a=0,∴a=-2.
(2)∵直线m恒过定点(0,9),先求直线m是曲线y=g(x)的切线,设切点为(x0,3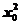 +6x0+12),
+6x0+12),
∵g′(x0)=6x0+6,
∴切线方程为y-(3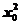 +6x0+12)=(6x0+6)(x-x0),将点(0,9)代入,得x0=±1,
+6x0+12)=(6x0+6)(x-x0),将点(0,9)代入,得x0=±1,
当x0=-1时,切线方程为y=9;
当x0=1时,切线方程为y=12x+9.
由f′(x)=0得-6x2+6x+12=0,即有x=-1或x=2,
当x=-1时,y=f(x)的切线方程为y=-18;
当x=2时,y=f(x)的切线方程为y=9.
∴公切线是y=9.
又有f′(x)=12得-6x2+6x+12=12,∴x=0或x=1.
当x=0时,y=f(x)的切线方程为y=12x-11;
当x=1时,y=f(x)的切线方程为y=12x-10,
∴公切线不是y=12x+9.
综上所述公切线是y=9,此时存在,k=0.
11.(文)(2010·开原模拟)设a>0,f(x)=a2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为[0,],则点P到曲线y=f(x)对称轴距离的取值范围为( )
A.[0,] B.[0,] C.[0,||] D.[0,||]
解析:∵y=f(x)在点P(x0,f(x0))处切线的倾斜角的范围为[0,],∴0≤f′(x0)≤1,即0≤2ax0+b≤1,∴-≤x0≤,∴0≤x0+≤,即点P到曲线y=f(x)对称轴的距离的取值范围为[0,].
答案:B
(理)曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是 ( )
A. B.2 C.3 D.0
解析:设曲线上过点P(x0,y0)的切线平行于直线2x-y+3=0,此切点到直线2x-y+3=0的距离最短,即斜率是2,则
y′|x=x0=[·(2x-1)′]|x=x0
=|x=x0==2.
解得x0=1,所以y0=0,即点P(1,0),
点P到直线2x-y+3=0的距离为=,
∴曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是.
答案:A
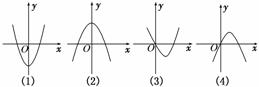
10.下图中,有一个是函数f(x)=x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)= ( )
A.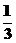 B.-
C.
B.-
C.  D.-或
D.-或
解析:∵f′(x)=x2+2ax+(a2-1),
∴导函数f′(x)的图象开口向上.
又∵a≠0,∴其图象必为第(3)个图.
由图象特征知f′(0)=0,且-a>0,∴a=-1.
故f(-1)=--1+1=-.
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com