10.已知函数f(x)＝x²－2ax+a，在区间(－∞，1)上有最小值，则函数g(x)＝在区间(1，+∞)上一定　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.有最小值 　　　B.有最大值　　 C.是减函数 　　　　D.是增函数

解析：由题意a<1，又函数g(x)＝x+－2a在[，+∞)上为增函数，故选D.

答案：D

9.设奇函数f(x)在 [－1,1]上是增函数，f(－1)＝－1.若函数f(x)≤t²－2at+1对所有的x∈[－1,1]都成立，则当a∈[－1,1]时，t的取值范围是　　.

解析：若函数f(x)≤t²－2at+1对所有的x∈[－1,1]都成立，由已知易得f(x)的最大值是1，

∴1≤t²－2at+1⇔2at－t²≤0，

设g(a)＝2at－t²(－1≤a≤1)，欲使2at－t²≤0恒成立，

则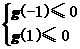⇔t≥2或t＝0或t≤－2.

答案：t≤－2或t＝0或t≥2

8.(2009·四川高考)已知函数f(x)是定义在实数集R上的不恒为零的偶函数，且对任意实数x都有xf(x+1)＝(1+x)f(x)，则f()的值是　　　　　　　　　　　　　　　 (　)

A.0 　　　　　　B.　　　　　　 C.1 　　　　　　　　D.

解析：令x＝－，∴－f()＝f(－)＝f()

(∵f(－)＝f())，∴f()＝0.

令x＝，∴f()＝f()，∴f()＝0.

令x＝，∴f()＝f()，∴f()＝0.

答案：A

7.已知f (x)是定义在(－∞，+∞)上的偶函数，且在(－∞，0]上是增函数，设a＝f (log₄7)，b＝f (log3)，c＝f (0.2^0.6)，则a，b，c的大小关系是　　　　　　　　　　　　 (　)

A.c<b<a　 　　　　B.b<c<a　　　　　 C.c>a>b 　　　　　　　D.a<b<c

解析：由题意f (x)＝f (|x|).

∵log₄7＝log₂>1，|log3|＝log₂3>1,0<0.2^0.6<1，

∴|log3|>|log₄7|>|0.2^0.6|.

又∵f(x)在(－∞，0]上是增函数且为偶函数，

∴f(x)在[0，+∞)上是减函数.∴c>a>b.

答案：C

6.已知函数f (x)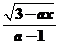＝ (a≠1).

(1)若a＞0，则f (x)的定义域是　　；

(2)若f (x)在区间(0,1]上是减函数，则实数a的取值范围是　　.

解析：当a＞0且a≠1时，由3－ax≥0得x≤，即此时函数f(x)的定义域是(－∞，]；

(2)当a－1＞0，即a＞1时，要使f(x)在(0,1]上是减函数，则需3－a×1≥0，此时1＜a≤3.

当a－1＜0，即a＜1时，要使f(x)在(0,1]上是减函数，则需－a＞0，

此时a＜0.

综上所述，所求实数a的取值范围是(－∞，0)∪(1,3].

答案：(1)(－∞，]　(2)(－∞，0)∪(1,3]

5.(2010·黄冈模拟)已知函数f(x)＝ (2x²+x)，则f (x)的单调递增区间为　　 　(　)

A.(－∞，－) 　　B.(－，+∞)　　 C.(0，+∞)　　 　D.(－∞，－)

解析：由2 x ²+x＞0，得x＞0或x＜－，

令h(x)＝2 x ²+x，则h(x)的单调减区间为(－∞，－).

又∵x <－，

∴f (x)的单调递增区间为(－∞，－).

答案：D

4.如果函数f (x)＝x²+2(a－1)x+2在区间(－∞，4]上是减函数，则实数a的取值范围是

(　)

A.[－3，+∞)　 　B.(－∞，－3]　　 C.(－∞，5]　 　　D.[3，+∞)

解析：f(x)＝x²+2(a－1)x+2的对称轴为x＝1－a，

∴f (x)在(－∞，1－a]上是减函数，要使f(x)在区间(－∞，4]上是减函数，则只需1－a≥4，即a≤－3.

答案：B

3.讨论函数f(x)＝x+(a>0)的单调性.

解：f(x)＝x+(a>0)，

∵定义域为{x|x∈R，且x≠0}且

f (－x)＝－x+＝－(x+)＝－f (x).

∴f (x)为奇函数，

所以先讨论f (x)在(0，+∞)上的单调性.

设x ₁> x ₂>0，

则f (x ₁)－f (x₂)＝x₁+－x₂－＝(x₁－x₂)(1－)，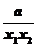

∵当0<x₂<x₁≤时，恒有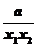>1.

则f (x₁)－f (x₂)<0，故f (x)在(0，]上是减函数.

当x₁>x₂≥时，恒有0<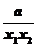<1，

则f (x₁)－f (x₂)>0，故f (x)在[，+∞)上是增函数.

∵f (x)是奇函数，

∴f (x)在(－∞，－]，[，+∞)上为增函数；

f (x)在[－，0)，(0，]上为减函数.

2.函数y＝x²+b x+c(x∈[0，+∞))是单调函数的充要条件是　　　　　　　　　 (　)

A.b≥0　 　B.b≤0 　　　C. b＞0　 　　　D. b＜0

解析：∵函数y＝x²+bx+c在[0，+∞)上为单调函数

∴x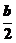＝－≤0，即b≥0.

答案：A

1.(2009·福建高考)下列函数f(x)中，满足“对任意x₁，x₂∈(0，+∞)，当x₁<x₂时，都有f(x₁)>f(x₂)”的是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.f(x)＝ 　　　　　　　　　　　　　B.f(x)＝(x－1)²

C.f(x)＝e^x　 　　　　　　　　　　　　D.f(x)＝ln(x+1)

解析：∵对任意的x₁，x₂∈(0，+∞)，当x₁<x₂时，

都有f(x₁)>f(x₂)，∴f(x)在(0，+∞)上为减函数.

答案：A