
6.(2010·包头模拟)已知下列曲线:
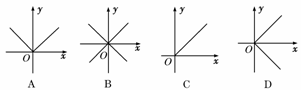
以及编号为①②③④的四个方程:
①-=0;②|x|-|y|=0;③x-|y|=0;④|x|-y=0.
请按曲线A、B、C、D的顺序,依次写出与之对应的方程的编号 .
解析:按图象逐个分析,注意x、y的取值范围.
答案:④②①③
5.函数f(x)=·ax(a>1)图象的大致形状是 ( )
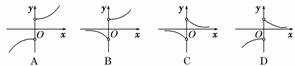
解析:f(x)是分段函数,根据x的正负写出分段函数的解析式,f(x)=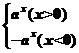 ,∴x>0时,图象与y=ax在第一象限的图象一样,x<0时,图象与y=ax的图象关于x轴对称,故选B.
,∴x>0时,图象与y=ax在第一象限的图象一样,x<0时,图象与y=ax的图象关于x轴对称,故选B.
答案:B
4.函数y=1-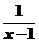 的图象是
( )
的图象是
( )
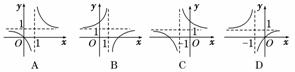
解析:法一:将函数y= 的图象变形到y=
的图象变形到y=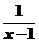 ,即向右平移1个单位,再变形到y=-
,即向右平移1个单位,再变形到y=-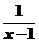 ,即将前面图形沿x轴翻转,再变形到y=-
,即将前面图形沿x轴翻转,再变形到y=-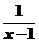 +1,从而得到答案B.
+1,从而得到答案B.
法二:利用特殊值法,取x1=0,此时y1=2;取x2=2,此时y2=0.因此选B.
答案:B
3.作出下列函数的图象:
(1)y=|x-2|·(x+1);
(2)y=()|x|;
(3)y=|log2(x+1)|.
解:(1)先化简,再作图.
y=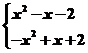 如图(1).
如图(1).
(2)此函数为偶函数,
利用y=()x(x≥0)的图象进行变换.如图(2).
(3)利用y=log2x的图象进行平移和翻折变换.
如图(3).

|
题组二 |
识 图 |
2.函数f(x)=1+log2x与g(x)=21-x在同一直角坐标系下的图象大致是 ( )
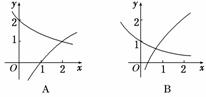
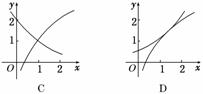
解析:利用函数的平移可画出所给函数的图象,函数f(x)=1+log2x的图象是由f(x)=log2x的图象向上平移1个单位得到;而g(x)=2-x+1=2-(x-1)的图象是由y=2-x的图象右移1个单位而得.
答案:C
1.为了得到函数y=3×()x的图象,可以把函数y= ()x的图象 ( )
A.向左平移3个单位长度
B.向右平移3个单位长度
C.向左平移1个单位长度
D.向右平移1个单位长度
解析:∵y=3×()x=()x-1,
∴y=3×()x的图象可以把函数y=()x的图象向右平移1个单位.
答案:D
12.(文)已知函数f(x)=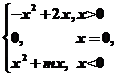 是奇函数.
是奇函数.
(1)求实数m的值;
(2)若函数f(x)的区间[-1,a-2]上单调递增,求实数a的取值范围.
解:(1)设x<0,则-x>0,
所以f(-x)=-(-x)2+2(-x)=-x2-2x.
又f(x)为奇函数,所以f(-x)=-f(x),
于是x<0时,f(x)=x2+2x=x2+mx,
所以m=2.
 (2)要使f(x)在[-1,a-2]上单调递增,
(2)要使f(x)在[-1,a-2]上单调递增,
结合f(x)的图象知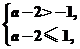
所以1<a≤3,故实数a的取值范围是(1,3].
(理)已知定义域为R的函数f(x)=是奇函数.
(1)求a、b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
解:(1)因为f(x)是R上的奇函数,所以f(0)=0,
即=0,解得b=1,从而有f(x)=.
又由f(1)=-f(-1),知=-,解得a=2.
故a=2,b=1.
(2)由(1)知f(x)==-+.
由上式易知f(x)在(-∞,+∞)上为减函数.
又因f(x)是奇函数,
从而不等式f(t2-2t)+f(2t2-k)<0
等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k).
因f(x)是减函数,由上式推得t2-2t>-2t2+k,
即对一切t∈R有3t2-2t-k>0.
从而判别式Δ=4+12k<0,解得k<-.
11.(2009·山东高考)已知定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2] 上是增函数.若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4, 则x1+x2+x3+x4= .
解析:由f(x-4)=-f(x)⇒f(4-x)=f(x),
故函数图象关于直线x=2对称,
又函数f(x)在[0,2]上是增函数,且为奇函数,
故f(0)=0,故函数f(x)在(0,2]上大于0,
根据对称性知函数f(x)在[2,4)上大于0,
同理推知函数f(x)在(4,8)上小于0,故在区间(0,8)上方程f(x)=m(m>0)的两根关于 直线x=2对称,
故此两根之和等于4,
根据f(x-4)=-f(x)⇒f(x-8)=-f(x-4)=f(x),
函数f(x)以8为周期,
故在区间(-8,0)上方程f(x)=m(m>0)的两根关于直线x=-6对称,此两根之和等 于-12,
综上四个根之和等于-8.
答案:-8
10.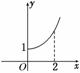 (2009·福建高考)定义在R上的偶函数f(x)的部分图象如右图所示,
(2009·福建高考)定义在R上的偶函数f(x)的部分图象如右图所示,
则在(-2,0)上,下列函数中与f(x)的单调性不同的是 ( )
A.y=x2+1
B.y=|x|+1
C.y=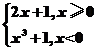
D.y=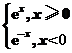
解析:∵f(x)为偶函数,由图象知,
f(x)在(-2,0)上为减函数,
而y=x3+1在(-∞,0)上为增函数,故选C.
答案:C
9.定义在R上的偶函数f(x),对任意x1,x2∈[0,+∞)(x1≠x2),有<0,则( )
A.f(3)<f(-2)<f(1) B.f(1)<f(-2)<f(3)
C.f(-2)<f(1)<f(3) D.f(3)<f(1)<f(-2)
解析:由已知<0,得f(x)在x∈[0,+∞)上单调递减,由偶函数性质得f(3)<f(-2)<f(1),故选A.此类题能用数形结合更好.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com