12.(文)若f(x)＝x²－x+b，且f(log₂a)＝b，log₂f(a)＝2(a>0且a≠1).

(1)求f(log₂x)的最小值及相应x的值；

(2)若f(log₂x)>f(1)且log₂f(x)<f(1)，求x的取值范围.

解：(1)∵f(x)＝x²－x+b，

∴f(log₂a)＝(log₂a)²－log₂a+b＝b，

∴log₂a＝1，∴a＝2.

又∵log₂f(a)＝2，∴f(a)＝4.∴a²－a+b＝4，∴b＝2.

∴f(x)＝x²－x+2.

∴f(log₂x)＝(log₂x)²－log₂x+2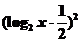＝²+.

∴当log₂x＝，即x＝时，f(log₂x)有最小值.

(2)由题意知

(理)已知f(x)＝log_ax，g(x)＝2log_a(2x+t－2)(a>0，a≠1，t∈R).

(1)当t＝4，x∈[1,2]，且F(x)＝g(x)－f(x)有最小值2时，求a的值；

(2)当0<a<1，x∈[1,2]时，有f(x)≥g(x)恒成立，求实数t的取值范围.

解：(1)当t＝4时，

F(x)＝g(x)－f(x)＝log_a，x∈[1,2]，

令h(x)＝＝4(x++2)，x∈[1,2]，则

h′(x)＝4(1－)＝>0，

∴h(x)在[1,2]上是单调增函数，

∴h(x)_min＝16，h(x)_max＝18.

当0<a<1时，有F(x)_min＝log_a18，

令log_a18＝2求得a＝3>1(舍去)；

当a>1时，有F(x)_min＝log_a16，

令log_a16＝2求得a＝4>1.∴a＝4.

(2)当0<a<1，x∈[1,2]时，有f(x)≥g(x)恒成立，

即当0<a<1，x∈[1,2]时，log_ax≥2log_a(2x+t－2)恒成立，

由log_ax≥2log_a(2x+t－2)可得log_a≥log_a(2x+t－2)，

∴≤2x+t－2，∴t≥－2x++2.

设u(x)＝－2x++2＝－2()²++2

＝－2(－)²+，

∵x∈[1,2]，∴∈[1，].

∴u(x)_max＝u(1)＝1.

∴实数t的取值范围为t≥1.

11.若函数f(x)＝log_a(2x²+x)(a＞0，a≠1)在区间(0，)内恒有f(x)＞0，则f(x)的单调递增区间是　　.

解析：定义域为(0，+∞)∪(－∞，－)，当x∈(0，)时，2x²+x∈(0,1)，因为a＞ 0，a≠1，设u＝2x²+x＞0，y＝log_au在(0,1)上大于0恒成立，∴0＜a＜1，所以函数f(x)＝log_a(2x²+x)(a＞0，a≠1)的单调递增区间是u＝2x²+x(x∈(－∞，－)∪(0，+∞))的递减区间，即(－∞，－).

答案：(－∞，－)

10.(2009·辽宁高考)已知函数f(x)满足：当x≥4时，f(x)＝()^x；当x＜4时，f(x)＝f(x+1).则f(2+log₂3)＝　　　　　　　　　　 　　　　　　　　　　　　　　　(　)

A. 　　　B.　　　　 C.　 　　　　　D.

解析：∵2＜3＜4＝2²，∴1＜log₂3＜2.

∴3＜2+log₂3＜4，

∴f(2+log₂3)＝f(3+log₂3)＝f(log₂24)

＝＝＝＝.

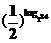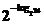答案：A

9.已知f(x)＝log_a(ax²－x)(a＞0，且a≠1)在区间[2,4]上是增函数，求实数a的取值范围.

解：设t＝ax²－x＝a(x－)²－，

若f(x)＝log_at在[2,4]上是增函数，

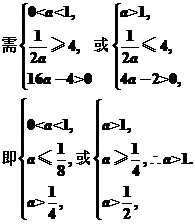
所以实数a的取值范围为(1，+∞).

8.(文)函数f(x)＝a^x+log_a(x+1)在[0,1]上的最大值与最小值之和为a，则a的值为(　)

A. 　　　B.　　　 C. 2　　　　 　D. 4

解析：故y＝a^x与y＝log_a(x+1)单调性相同且在[0,1]上的最值分别在两端点处取得.

最值之和：f(0)+f(1)＝a⁰+log_a1+a+log_a2＝a，

∴log_a2+1＝0，∴a＝.

答案：B

(理)函数f(x)＝a^x+log_ax在区间[1,2]上的最大值与最小值之和为－，最大值与最小值之积为－，则a等于　　　　　　　　　　 　　　　　　　　　　　　　　(　)

A.2　 　　　B.　　　 C.2或 　　　　　D.

解析：a^x与log_ax具有相同的单调性，最大值与最小值在区间的端点处取得，f(1)+f(2)＝－，f(1)·f(2)＝－，解得a＝.

答案：B

7.(2010·诸城模拟)若定义运算f(a*b)＝　　　　　 则函数f[log₂(1+x)*log₂(1－x)]的值域是　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　)

A.(－1,1)　 　　B.[0,1)　　　　 C.(－∞，0]　 　　　　　D.[0，+∞)

解析：f(log₂(1+x)*log₂(1－x))

＝

借助函数图象易知，该函数的值域为[0,1).

答案：B

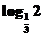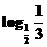6.(2009·天津高考)设a＝，b＝，c＝()^0.3，则　　　　　　　　 (　)

A.a＜b＜c 　　B.a＜c＜b　　 C.b＜c＜a 　　　D.b＜a＜c

解析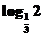：∵＜＝0，∴a＜0；

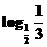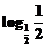∵＞＝1，∴b＞1；

∵()^0.3＜1，∴0＜c＜1，故选B.

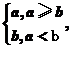
答案：B

5.已知函数f(x)＝ g(x)＝lnx，则f(x)与g(x)两函数的图象的交点

个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　(　)

A.1 　　　　B.2 　　　　　C.3 　　　　　　D.4

解析：画出f(x)＝

g(x)＝lnx的图象如图，两函数的图象的交点个数为3，故选C.

答案：C

4.若函数f(x)＝log_a(x+b)的图象如图所示，其中a，b为常数，则函数g(x)＝a^x+b的大致图象是　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　(　)

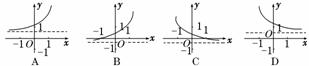
解析：由题意得0＜a＜1,0＜b＜1，则函数g(x)＝a^x+b的大致图象是D.

答案：D

3.(2009·广东高考)若函数y＝f(x)是函数y＝a^x(a＞0，且a≠1)的反函数，其图象经过点(，a)，则f(x)＝　　　　　　　　　　　　　　　　 　　　　　　　　　　　(　)

A.log₂x　 　　　B.　　　　 C.logx　　　　 　D.x²

解析：由题意f(x)＝log_ax，∴a＝log_aa＝，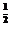

∴f(x)＝logx.

答案：C