8.已知函数f(x)＝x|x－4|－5，则当方程f(x)＝a有三个根时，实数a的取值范围是　　.

A.－5＜a＜－1　 　　B.－5≤a≤－1 　　C.a＜－5　　 　D.a＞－1

解析：f(x)＝x|x－4|－5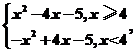＝在平面直角坐标系中画出该函数的图象(图略)，可得当直线y＝a与该函数的图象有三个交点时，a的取值范围是－5<a<－1.

答案：A

7.若二次函数y＝ax²+bx+c中a·c<0，则函数的零点个数是　　　　　 (　)

A.1个　 　　B.2个　　 C.0个 　　　D.不确定

解析：∵c＝f(0)，∴ac＝a·f(0)<0.

∴a与f(0)异号，即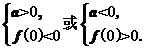

∴函数必有两个零点.

答案：B

6.设函数f(x)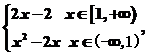＝则函数F(x)＝f(x)－的零点是　　.

解析：当x≥1时，f(x)－＝2x－2－＝2x－＝0，

∴x＝.

当x＜1时，x²－2x－＝0，

∵Δ＝4+1＞0，

∴x＝＝，又∵x＜1，∴x＝.

∴函数F(x)＝f(x)－有两个零点和.

答案：，

5.f(x)是定义在R上的以3为周期的偶函数，且f(2)＝0，则方程f(x)＝0在区间(0,6)内解的个数的最小值是　　　　　　　　　　 　　　　　　　　　　　　　　　　(　)

A.5　 　　　B.4 　　　C.3 　　　　　D.2

解析：∵f(x)是定义在R上的偶函数，且周期是3，f(2)＝0，∴f(2)＝f(5)＝f(－2)＝f(1)＝f(4)＝0.

答案：B

4.(2009·福建高考)若函数f(x)的零点与g(x)＝4^x+2x－2的零点之差的绝对值不超过0.25，则f(x)可以是　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.f(x)＝4x－1 　　　　　　　　　B.f(x)＝(x－1)²

C.f(x)＝e^x－1　 　　　　　　　　D.f(x)＝ln(x－)

解析：∵4个选项中的零点是确定的.

A：x＝；B：x＝1；C：x＝0；D：x＝.

又∵g(0)＝4⁰+2×0－2＝－1＜0，

g()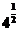＝+2×－2＝1＞0，

∴g(x)＝4^x+2x－2的零点介于(0，)之间.从而选A.

答案：A

3.(2010·苏北三市联考)若方程lnx+2x－10＝0的解为x₀，则不小于x₀的小整数是　　.

解析：令f(x)＝lnx+2x－10，

则f(5)＝ln5＞0，f(4)＝ln4－2＜0

∴4＜x₀＜5

∴不小于x₀的最小整数是5.

答案：5

2.设f(x)＝3^x－x²，则在下列区间中，使函数f(x)有零点的区间是　　　　　　　 (　)

A.[0,1] 　　　　　　　　　　　　B.[1,2]

C.[－2，－1] 　　　　　　　　　D.[－1,0]

解析：∵f(－1)＝3^－1－(－1)²＝－1＝－<0，

f(0)＝3⁰－0＝1>0，

∴函数f(x)＝3^x－x²在区间[－1,0]内存在零点.

答案：D

1.若函数f(x)在区间[－2,2]上的图象是连续不断的曲线，且函数f(x)在(－2,2)内有一个零点，则f(－2)·f(2)的值　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.大于0　 　　B.小于0 　　C.等于0 　　　D.不能确定

解析：若函数f(x)在(－2,2)内有一个零点，则该零点是变号零点，则f(－2)f(2)<0.若不是变号零点，则f(－2)f(2)>0.

答案：D

12.设f(x)＝ax²+bx+c，若6a+2b+c＝0，f(1)·f(3)＞0，

(1)若a＝1，求f(2)的值；

(2)求证：方程f(x)＝0必有两个不等实根x₁、x₂，且3＜x₁+x₂＜5.

解：(1)∵6a+2b+c＝0，a＝1，

∴f(2)＝4a+2b+c＝－2a＝－2.

(2)证明：首先说明a≠0，

∵f(1)·f(3)＝(a+b+c)(9a+3b+c)＝－(5a+b)(3a+b)＞0，

若a＝0，则f(1)·f(3)＝－b²＜0与已知矛盾，

∴a≠0，

其次说明二次方程f(x)＝0必有两个不等实根x₁、x₂，

∵f(2)＝4a+2b+c＝－2a，

∴若a＞0，二次函数f(x)＝ax²+bx+c开口向上，而此时f(2)＜0，

∴若a＜0，二次函数f(x)＝ax²+bx+c开口向下，而此时f(2)＞0.

故二次函数图象必与x轴有两个不同交点，

∴ 二次方程f(x)＝0必有两个不等实根x₁、x₂，

(或利用Δ＝b²－4ac＝b²+4a(6a+2b)＝b²+8ab+24a²＝(b+4a)²+8a²＞0来说明)

∵a≠0，

∴将不等式－(5a+b)(3a+b)＞0两边同除以－a²得

(+3)(+5)＜0，

∴－5＜＜－3.

∴3＜x₁+x₂＝－＜5.

11.不等式(a－2)x²+2(a－2)x－4＜0对一切x∈R恒成立，则a的取值范围是　　.

解析：当a－2＝0，即a＝2时，－4＜0恒成立；

当a－2≠0时，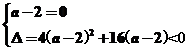　

解之得：－2＜a＜2

∴a的取值范围是－2＜a≤2.

答案：(－2,2]