8．某科研单位欲拿出一定的经费奖励科研人员，第1名得全部资金的一半多一万元，第二名得剩下的一半多一万元，以名次类推都得到剩下的一半多一万元，到第10名恰好资金分完，则此科研单位共拿出__________万元资金进行奖励．

解析：设第10名到第1名得的奖金数分别是a₁，a₂，…，a₁₀，则a_n＝S_n+1，则a₁＝2，a_n－a_n－1＝a_n，即a_n＝2a_n－1，因此每人得的奖金额组成以2为首项，以2为公比的等比数列，所以S₁₀＝＝2046.

答案：2046

7.有一种细菌和一种病毒，每个细菌在每秒钟杀死一个病毒的同时将自身分裂为2个，现在有一个这样的细菌和100个这样的病毒，问细菌将病毒全部杀死至少需要(　)

A．6秒钟 　　　　B．7秒钟　　　　 C．8秒钟 　　　D．9秒钟

解析：设至少需要n秒钟，则1+2¹+2²+…+2^n－1≥100，

∴≥100，∴n≥7.

答案：B

6．数列{a_n}中，a₁＝6，且a_n－a_n－1＝+n+1(n∈N^*，n≥2)，则这个数列的通项a_n＝________.

解析：由已知等式得na_n＝(n+1)a_n－1+n(n+1)(n∈N^*，n≥2)，则－＝1，所以数列{}是以＝3为首项，1为公差的等差数列，即＝n+2，则a_n＝(n+1)(n+2)．n＝1时，此式也成立．

答案：(n+1)(n+2)

5．(2010·邯郸模拟)若数列{a_n}满足－＝d(n∈N^*，d为常数)，则称数列{a_n}为调和数列．已知数列{}为调和数列，且x₁+x₂+…+x₂₀＝200，则x₅+x₁₆＝________.

解析：由题意，若{a_n}为调和数列，则{}为等差数列，所以{}为调和数列，则可得数列{x_n}为等差数列，由等差数列的性质可知，x₅+x₁₆＝x₁+x₂₀＝x₂+x₁₉＝…＝＝20.

答案：20

4.气象学院用3.2万元买了一台天文观测仪，已知这台观测仪从启用的第一天起连续使用，第n天的维修保养费为元(n∈N₊)，使用它直至报废最合算(所谓报废最合算是指使用的这台仪器的平均耗资最少)为止，一共使用了　　　　　　　　 (　)

A．600天　 　　　　B．800天　　　　 C．1 000天　　　　 　D．1 200天

解析：由第n天的维修保养费为元(n∈N₊)，可以得出观测仪的整个耗资费用，由平均费用最少而求得最小值成立时相应n的值．

设一共使用了n天，则使用n天的平均耗资为

＝++4.95，当且仅当＝时，取得最小值，此时n＝800.

答案：B

3．(文)已知等差数列{a_n}的前n项和为S_n且满足a₂＝3，S₆＝36.

(1)求数列{a_n}的通项公式；

(2)若数列{b_n}是等比数列且满足b₁+b₂＝3，b₄+b₅＝24.设数列{a_n·b_n}的前n项和为T_n，求T_n.

解：(1)∵数列{a_n}是等差数列，

∴S₆＝3(a₁+a₆)＝3(a₂+a₅)＝36.

∵a₂＝3，∴a₅＝9，∴3d＝a₅－a₂＝6，∴d＝2，

又∵a₁＝a₂－d＝1，∴a_n＝2n－1.

(2)由等比数列{b_n}满足b₁+b₂＝3，b₄+b₅＝24，

得＝q³＝8，∴q＝2，

∵b₁+b₂＝3，∴b₁+b₁q＝3，∴b₁＝1，b_n＝2^n－1，

∴a_n·b_n＝(2n－1)·2^n－1.

∴T_n＝1×1+3×2+5×2²+…+(2n－3)·2^n－2+(2n－1)·2^n－1，

则2T_n＝1×2+3×2²+5×2³+…+(2n－3)·2^n－1+(2n－1)·2ⁿ，

两式相减得(1－2)T_n＝1×1+2×2+2×2²+…+2·2^n－2+2·2^n－1－(2n－1)·2ⁿ，即

－T_n＝1+2(2¹+2²+…+2^n－1)－(2n－1)·2ⁿ

＝1+2(2ⁿ－2)－(2n－1)·2ⁿ＝(3－2n)·2ⁿ－3，

∴T_n＝(2n－3)·2ⁿ+3.

(理)已知数列{a_n}的前n项和为S_n，a₁＝1，数列{a_n+S_n}是公差为2的等差数列．

(1)求a₂，a₃；

(2)证明：数列{a_n－2}为等比数列；

(3)求数列{na_n}的前n项和T_n.

解：(1)∵数列{a_n+S_n}是公差为2的等差数列，

∴(a_n+1+S_n+1)－(a_n+S_n)＝2，即a_n+1＝.

∵a₁＝1，∴a₂＝，a₃＝.

(2)证明：由题意得a₁－2＝－1，

又∵＝＝，

∴{a_n－2}是首项为－1，公比为的等比数列．

(3)由(2)得a_n－2＝－()^n－1，∴na_n＝2n－n·()^n－1，

∴T_n＝(2－1)+(4－2·)+[6－3·()²]+…+[2n－n·()^n－1]，

＝(2+4+6+…+2n)－[1+2·+3·()²+…+n·()^n－1]，

设A_n＝1+2·+3·()²+…+n·()^n－1，　　　　　　　　　　　　　　　　　　　　 ①

∴A_n＝+2·()²+3·()³+…+n·()ⁿ，　　　　　　　　　　　　　　　　　　　 ②

①－②得A_n＝1++()²+…+()^n－1－n·()ⁿ，

∴A_n＝－n·()ⁿ，

∴A_n＝4－(n+2)·()^n－1，

∴T_n＝+(n+2)·()^n－1－4＝(n+2)·()^n－1+n(n+1)－4.

2．数列{a_n}是各项均为正数的等比数列，{b_n}是等差数列，且a₆＝b₇，则有　　　 (　)

A．a₃+a₉≤b₄+b₁₀

B．a₃+a₉≥b₄+b₁₀

C．a₃+a₉≠b₄+b₁₀

D．a₃+a₉与b₄+b₁₀的大小不确定

解析：∵a₃+a₉≥2＝2＝2a₆＝2b₇＝b₄+b₁₀，当且仅当a₃＝a₉时，不等式取等号．

答案：B

1.已知a，b，c成等比数列，a，m，b和b，n，c分别成两个等差数列，则+等于　 (　)

A．4　　　 B．3　　　　　　　 C．2 　　　　　　　D．1

解析：由题意得b²＝ac,2m＝a+b,2n＝b+c，则+＝＝＝＝2.

答案：C

12．(文)(2009·湖北高考改编)已知数列{a_n}的前n项和S_n＝－a_n－()^n－1+2(n∈N^*)．

(1)令b_n＝2ⁿa_n，求证数列{b_n}是等差数列，并求数列{a_n}的通项公式；

(2)令c_n＝a_n，求T_n＝c₁+c₂+…+c_n的值．

解：(1)在S_n＝－a_n－()^n－1+2中，

令n＝1，可得S₁＝－a₁－1+2＝a₁，即a₁＝.

当n≥2时，S_n－1＝－a_n－1－()^n－2+2，

∴a_n＝S_n－S_n－1＝－a_n+a_n－1+()^n－1，

∴2a_n＝a_n－1+()^n－1，即2ⁿa_n＝2^n－1a_n－1+1.

∵b_n＝2ⁿa_n，∴b_n＝b_n－1+1，

即当n≥2时，b_n－b_n－1＝1.

又b₁＝2a₁＝1，

∴数列{b_n}是首项和公差均为1的等差数列．

于是b_n＝1+(n－1)·1＝n＝2ⁿa_n，

∴a_n＝.

(2)由(1)得c_n＝a_n＝(n+1)()ⁿ，所以

T_n＝2×+3×()²+4×()³+…+(n+1)·()ⁿ，　　　　　　　　　　　　　　 ①

T_n＝2×()²+3×()³+…+n·()ⁿ+(n+1)·()ⁿ⁺¹，　　　　　　　　　　　　　 ②

由①－②得T_n＝1+()²+()³+…+()ⁿ－(n+1)·()ⁿ⁺¹

＝1+－(n+1)()ⁿ⁺¹

＝－.

∴T_n＝3－.

(理)已知数列{a_n}是首项为a₁＝，公比q＝的等比数列，设b_n+2＝3loga_n(n∈N^*)，数列{c_n}满足c_n＝a_n·b_n.

(1)求证：{b_n}是等差数列；

(2)求数列{c_n}的前n项和S_n；

(3)若c_n≤m²+m－1对一切正整数n恒成立，求实数m的取值范围．

解：(1)证明：由题意知，a_n＝()ⁿ(n∈N^*)．

∵b_n＝3log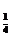a_n－2，b₁＝3log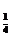a₁－2＝1，

∴b_n+1－b_n＝3log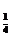a_n+1－3log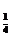a_n＝3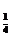log＝3log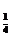q＝3，

∴数列{b_n}是首项为b₁＝1，公差为d＝3的等差数列．

(2)由(1)知，a_n＝()ⁿ，b_n＝3n－2(n∈N^*)，

∴c_n＝(3n－2)×()ⁿ，(n∈N^*)，

∴S_n＝1×+4×()²+7×()³+…+(3n－5)×()^n－1+(3n－2)×()ⁿ，

于是S_n＝1×()²+4×()³+7×()⁴+…+(3n－5)×()ⁿ+(3n－2)×()ⁿ⁺¹，

两式相减得

S_n＝+3[()²+()³+…+()ⁿ]－(3n－2)×()ⁿ⁺¹＝－(3n+2)×()ⁿ⁺¹，

∴S_n＝－·()ⁿ(n∈N^*)．

(3)∵c_n+1－c_n＝(3n+1)·()ⁿ⁺¹－(3n－2)·()ⁿ

＝9(1－n)·()ⁿ⁺¹，(n∈N^*)．

∴当n＝1时，c₂＝c₁＝，

当n≥2时，c_n+1＜c_n，即c₁＝c₂>c₃>c₄>…>c_n，

∴c_n取得的最大值是.

又c_n≤m²+m－1对一切正整数n恒成立，

∴m²+m－1≥，即m²+4m－5≥0，

得m≥1或m≤－5.

11．对于数列{a_n}，定义数列{a_n+1－a_n}为数列{a_n}的“差数列”，若a₁＝2，{a_n}的“差数列”的通项为2ⁿ，则数列{a_n}的前n项和S_n＝________.

解析：∵a_n+1－a_n＝2ⁿ，

∴a_n＝(a_n－a_n－1)+(a_n－1－a_n－2)+…+(a₂－a₁)+a₁

＝2^n－1+2^n－2+…+2²+2+2

＝+2＝2ⁿ－2+2＝2ⁿ.

∴S_n＝＝2ⁿ⁺¹－2.

答案：2ⁿ⁺¹－2