
7.(2009·湖南高考)对于非零向量a、b,“a+b=0”是“a∥b”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解析:由a+b=0知道a与b互为相反向量,从而a∥b,充分性成立. 由a∥b知a=λb.λ≠-1时,a+b≠0,∴必要性不成立.
答案:A
6.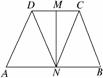 如图,若四边形ABCD是一个等腰梯形,AB∥DC,M、
如图,若四边形ABCD是一个等腰梯形,AB∥DC,M、
N分别是DC,AB的中点,已知=a,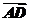 =b,
=b,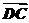 =
=
c,试用a,b,c表示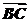 ,
,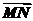 ,
,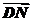 +
+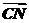 .
.
解: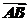 =
=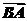 +
+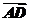 +
+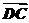 =-a+b+c.
=-a+b+c.
∵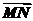 =
= +
+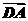 +
+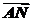 ,
,
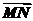 =
=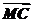 +
+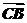 +
+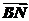 ,
,
∴2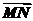 =
= +
+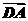 +
+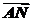 +
+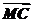 +
+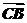 +
+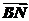 =
=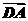 +
+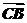 =-
=-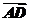 +
+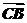 =-b-(-a+b+c)=a-2b-c,
=-b-(-a+b+c)=a-2b-c,
∴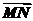
 =a-b-c.
=a-b-c.
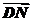 +
+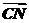 =
=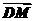 +
+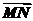 +
+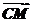 +
+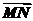
=2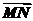 =a-2b-c.
=a-2b-c.
|
题组三 |
向量的共线问题 |
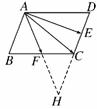
5.(2009·安徽高考)在平行四边形ABCD中,E和F分别是边CD和BC的中点.若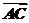 =λ
=λ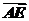 +μ
+μ ,其中,λ,μ∈R,则λ+μ=________.
,其中,λ,μ∈R,则λ+μ=________.
解析:如图,∵ABCD为▱,且E、F分别为CD、BC中点.
 ∴
∴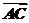 =
=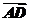 +
+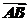
=(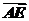 -
-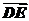 )+(
)+( -
-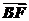 )
)
=(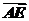 +
+ )-(
)-(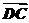 +
+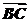 )
)
=(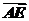 +
+ )-
)-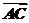 ,
,
∴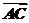 =(
=(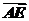 +
+ ),
),
∴λ=μ=,∴λ+μ=.
答案:
4.如图所示,D是△ABC的边AB的中点,则向量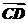 =
( )
=
( )
 A.-
A.- +
+ B.-
B.-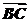 -
-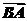
C.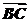 -
-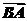 D.
D. 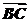 +
+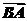
解析: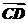 =
=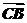 +
+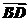 =-
=-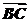 +
+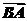 .
.
答案:A
3.若A、B、C、D是平面内任意四点,给出下列式子:①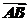 +
+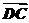 =
=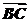 +
+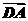 ;②
;②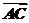 +
+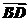 =
=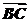 +
+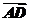 ;③
;③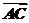 -
-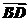 =
=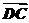 +
+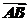 .其中正确的有
( )
.其中正确的有
( )
A.0个 B.1个 C.2个 D.3个
解析:①式的等价式是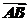 -
-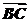 =
=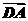 -
-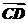 ,左边=
,左边=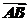 +
+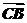 ,右边=
,右边=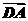 +
+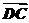 ,不一定相等;
,不一定相等;
②式的等价式是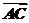 -
-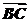 =
=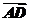 -
-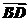 ,
,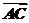 +
+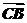 =
=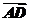 +
+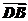 =
=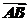 成立;
成立;
③式的等价式是-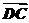 =
=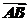 +
+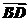 ,
,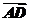 =
=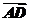 成立.
成立.
答案:C
2.下列四个命题,其中正确的个数有 ( )
①对于实数m和向量a,b,恒有m(a-b)=ma-mb
②对于实数m,n和向量a,恒有(m-n)a=ma-na
③若ma=mb(m∈R),则有a=b
④若ma=na(m,n∈R,a≠0),则有m=n
A.1个 B.2个 C.3个 D.4个
解析:只有③不正确,∵a≠b,m=0时,ma=mb也成立,其余①②④均成立.
答案:C
|
题组二 |
向量的线性运算 |
1.给出下列六个命题:
①两个向量相等,则它们的起点相同,终点相同;
②若|a|=|b|,则a=b;
③若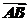 =
=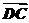 ,则四边形ABCD为平行四边形;
,则四边形ABCD为平行四边形;
④在▱ABCD中,一定有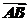 =
=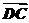 ;
;
⑤若m=n,n=p,则m=p;
⑥若a∥b,b∥c,则a∥c,
其中不正确的个数是 ( )
A.2 B.3 C.4 D.5
解析:两向量起点相同,终点相同,则两向量相等;但两相等向量,不一定有相同的起点和终点,故①不正确.|a|=|b|,由于a与b方向不确定,所以a,b不一定相等,故②不正确.零向量与任一向量平行,故a∥b,b∥c时,若b=0,则a与c不一定平行,故⑥不正确.正确的是③④⑤.
答案:B
8.某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
|
|
班级工作 积极参加 |
不太主动参加班级工作 |
合计 |
|
学习积极性高 |
18 |
7 |
25 |
|
学习积极性一般 |
6 |
19 |
25 |
|
合计 |
24 |
26 |
50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多
少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否
有关?并说明理由.
解:(1)积极参加班级工作的学生有24名,总人数为50名,概率为=.
不太主动参加班级工作且学习积极性一般的学生有19名,概率为.
(2)χ2==≈11.5,
∵χ2>6.635,
∴有99%的把握认为学习积极性与对待班级工作的态度有关系.
7.在一次飞机航程中调查男女乘客的晕机情况,其中,男性乘客80人中有10人晕机,女性乘客30人中有10人晕机.
(1)写出2×2列联表;
(2)判断晕机与性别是否有关?
解:(1)2×2列联表:
|
|
晕机 |
不晕机 |
合计 |
|
男 |
10 |
70 |
80 |
|
女 |
10 |
20 |
30 |
|
合计 |
20 |
90 |
110 |
(2)χ2=≈6.37>3.841,
故有95%的把握认为“晕机与性别有关”.
6.在一项打鼾与患心脏病的调查中,共调查了1671人,经过计算χ2=27.63,根据这一数据分析,我们有理由认为打鼾与患心脏病是________的(填“有关”或“无关”).
解析:χ2>6.635,有99%的把握说打鼾与患心脏病有关.
答案:有关
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com