
3.(2009·福建高考)设a,b,c为同一平面内具有相同起点的任意三个非零向量,且满足a与b不共线,a⊥c,|a|=|c|,则|b·c|的值一定等于 ( )
A.以a,b为两边的三角形的面积
B.以b,c为两边的三角形的面积
C.以a,b为邻边的平行四边形的面积
D.以b,c为邻边的平行四边形的面积
解析:设〈a,b〉=θ,θ∈(0,π),
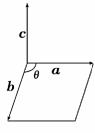 ∵〈a,c〉=,∴〈b,c〉=-θ,
∵〈a,c〉=,∴〈b,c〉=-θ,
以a,b为邻边的平行四边形面积为
|a||b|sinθ,而|b·c|=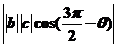
=|b||c|sinθ,
又|a|=|c|,∴|b·c|=|a||b|sinθ.
答案:C
|
题组二 |
两向量的夹角问题 |
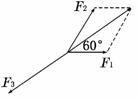
2.(2009·广东高考)一质点受到平面上的三个力F1、F2、F3(单位:牛顿)的作用而处于平衡状态.已知F1、F2成60°角,且F1、F2的大小分别为2和4,则F3的
大小为 ( )
A.2 B.2 C.2 D.6
解析:由已知得F1+F2+F3=0,∴F3=-(F1+F2).
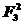 =
=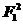 +
+ +2F1F2=
+2F1F2=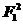 +
+ +2|F1||F2|cos60°=28.
+2|F1||F2|cos60°=28.
 ∴|F3|=2.
∴|F3|=2.
答案:A
1.(2010·四平模拟)设a、b、c是单位向量,且a·b=0,则(a-c)·(b-c)的最小值为 ( )
A.-2 B.-2 C.-1 D.1-
解析:(a-c)·(b-c)=a·b-c·(a+b)+c2
=0-|c|·|a+b|·cos〈c,(a+b)〉+1
≥0-| c ||a+b|+1=-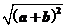 +1
+1
=-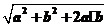 +1=-
+1=-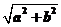 +1
+1
=-+1.
答案:D
12.如图所示,已知点A(4,0),B(4,4),C(2,6),求AC和OB交点P的坐标.
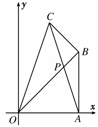 解:法一:设
解:法一:设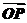 =t
=t =t(4,4)=(4t,4t),
=t(4,4)=(4t,4t),
则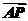 =
=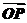 -
-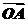 =(4t,4t)-(4,0)=(4t-4,4t),
=(4t,4t)-(4,0)=(4t-4,4t),
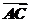 =(2,6)-(4,0)=(-2,6).
=(2,6)-(4,0)=(-2,6).
由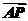 ,
,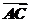 共线的充要条件知
共线的充要条件知
(4t-4)×6-4t×(-2)=0,解得t=.
∴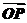 =(4t,4t)=(3,3).
=(4t,4t)=(3,3).
∴P点坐标为(3,3).
法二:设P(x,y),则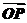 =(x,y),
=(x,y), =(4,4).
=(4,4).
∵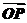 ,
, 共线,∴4x-4y=0.
①
共线,∴4x-4y=0.
①
又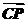 =(x-2,y-6),
=(x-2,y-6),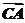 =(2,-6),
=(2,-6),
且向量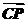 、
、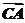 共线.
共线.
∴-6(x-2)+2(6-y)=0. ②
解①,②组成的方程组,得x=3,y=3,
∴点P的坐标为(3,3).
11.△ABC的三个内角,A,B,C所对的边长分别为a,b,c,若p=(a+c,b)与q=(b-a,c-a)是共线向量,则角C=________.
解析:∵p∥q,∴(a+c)(c-a)-b(b-a)=0,
∴a2+b2-c2=ab.
∴cosC==,∴C=60°.
答案:60°
10.在平面直角坐标系中,O为坐标原点,已知A(3,1),B(-1,3),若点C满足|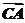 +
+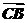 |=|
|=|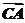 -
-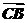 |,则C点的轨迹方程是
( )
|,则C点的轨迹方程是
( )
A.x+2y-5=0 B.2x-y=0
C.(x-1)2+(y-2)2=5 D.3x-2y-11=0
解析:由|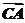 +
+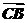 |=|
|=|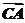 -
-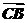 |知
|知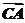 ⊥
⊥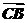 ,所以C点的轨迹是以A、B为直径的两个端点的圆,圆心坐标为线段AB的中点(1,2),半径等于,所以C点的轨迹方程是(x-1)2+(y-2)2=5.
,所以C点的轨迹是以A、B为直径的两个端点的圆,圆心坐标为线段AB的中点(1,2),半径等于,所以C点的轨迹方程是(x-1)2+(y-2)2=5.
答案:C
9.已知a=(3,2),b=(-1,2),c=(4,1).
(1)求满足a=xb+yc的实数x,y的值;
(2)若(a+kc)∥(2b-a),求实数k的值.
解:(1)∵a=xb+yc,
∴(3,2)=x(-1,2)+y(4,1)=(-x+4y,2x+y).
∴解得
(2)∵(a+kc)∥(2b-a),
且a+kc=(3,2)+k(4,1)=(3+4k,2+k),
2b-a=2(-1,2)-(3,2)=(-5,2),
∴2(3+4k)-(-5)(2+k)=0,解得k=-.
|
题组四 |
平面向量基本定理及坐标表示的综合应用 |
8.已知向量a=(1-sinθ,1),b=(,1+sinθ),且a∥b,则锐角θ等于 ( )
A.30° B.45° C.60° D.75°
解析:由a∥b可得(1-sinθ)(1+sinθ)-=0,即cosθ=±,而θ是锐角,故θ=45°.
答案:B
7.(2009·北京高考)已知向量a、b不共线,c=ka+b(k∈R),d=a-b.如果c∥d,那么( )
A.k=1且c与d同向
B.k=1且c与d反向
C.k=-1且c与d同向
D.k=-1且c与d反向
解析:不妨设a=(1,0),b=(0,1).依题意d=a-b=(1,-1),又c=ka+b=(k,1),∵c∥d,∴12-(-1)·k=0,
∴k=-1,又k=-1时,c=(-1,1)=-d,∴c与d反向.
答案:D
6.(2010·黄冈模拟)在平面直角坐标系中,O为坐标原点,设向量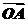 =a,
=a, =b,其中a=(3,1),b=(1,3).
=b,其中a=(3,1),b=(1,3).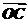 =λa+μb,且0≤λ≤μ≤1,C点所有可能的位置区域用阴影表正确的是
( )
=λa+μb,且0≤λ≤μ≤1,C点所有可能的位置区域用阴影表正确的是
( )
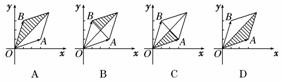
解析: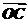 =λa+μb=λ(3,1)+μ(1,3)=(3λ+μ,λ+3μ).
=λa+μb=λ(3,1)+μ(1,3)=(3λ+μ,λ+3μ).
∵0≤λ≤μ≤1,
∴0≤3λ+μ≤4,0≤λ+3μ≤4,且3λ+μ≤λ+3μ.
答案:A
|
题组三 |
平行(共线)向量的坐标表示 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com