
7.已知两条互不平行的线段AB和A′B′关于直线1对称,AB和A′B′所在的直线交于点P,下面四个结论:①AB=A′B′;②点P在直线1上;③若A、A′是对应点,则直线1垂直平分线段AA′;④若B、B′是对应点,则PB=PB′,其中正确的是( )
A.①③④ B.③④ C.①② D.①②③④
6.已知M(a,3)和N(4,b)关于y轴对称,则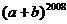 的值为( )
的值为( )
A.1 B、-1 C. D.
D.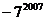
5.已知:如图3,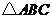 的顶点坐标分别为
的顶点坐标分别为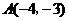 ,
,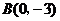 ,
,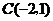 ,如将
,如将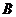 点向右平移2个单位后再向上平移4个单位到达
点向右平移2个单位后再向上平移4个单位到达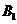 点,若设
点,若设 的面积为
的面积为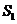 ,
, 的面积为
的面积为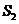 ,则
,则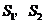 的大小关系为( )
的大小关系为( )
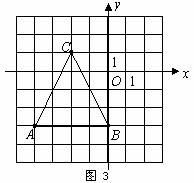 A.
A.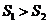 B.
B.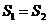
C.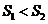 D.不能确定
D.不能确定
4.点M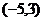 关于x轴的对称点的坐标是( )
关于x轴的对称点的坐标是( )
A. 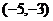 B.
B.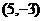 C.
C. D.
D.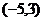
3.如图2,把一个正方形对折两次后沿虚线剪下,展开后所得的图形是

上折 右折 沿虚线剪开 展开
图 2
A. B. C. D.
2.在下列说法中,正确的是( ) A.如果两个三角形全等,则它们必是关于直线成轴对称的图形; B.如果两个三角形关于某直线成轴对称,那么它们是全等三角形; C.等腰三角形是关于底边中线成轴对称的图形; D.一条线段是关于经过该线段中点的直线成轴对称的图形
1.下列图案中是轴对称图形的有:

(A)1个 (B)2个 (C)3个 (D)4个
22.(本小题满分14分)已知△ABC的面积为S,满足≤S≤3,且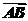 ·
·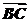 =6,
=6,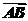 与
与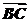 的夹角为θ.
的夹角为θ.
(1)求角θ的取值范围;
(2)求函数f(θ)=sin2θ+2sinθ·cosθ+3cos2θ的最小值.
解:(1)由题意知,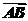 ·
·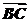 =|
=|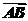 |·|
|·|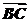 |cosθ=6,
①
|cosθ=6,
①
S=|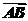 |·|
|·|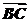 |sin(π-θ)=|
|sin(π-θ)=|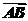 |·|
|·|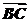 |sinθ,
②
|sinθ,
②
由,得=tanθ,即3tanθ=S.
由≤S≤3,得≤3tanθ≤3,
即≤tanθ≤1.
又θ为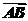 与
与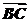 的夹角,
的夹角,
∴θ∈(0,π],∴θ∈[,].
(2)f(θ)=sin2θ+2sinθ·cosθ+3cos2θ
=1+sin2θ+2cos2θ
=2+sin2θ+cos2θ
=2+sin(2θ+).
∵θ∈[,],∴2θ+∈[,],
∴当2θ+=,即θ=时,f(θ)取得最小值为3.
21.(本小题满分12分)已知向量a=(cosx,sinx),b=(-cosx,cosx),c=(-1,0).
(1)若x=,求向量a,c的夹角;
(2)当x∈[,]时,求函数f(x)=2a·b+1的最大值.
解:(1)设a,c的夹角为θ,当x=时,
cos〈a,c〉==
=-cosx=-cos=cos.
∵0≤〈a,c〉≤π,∴〈a,c〉=.
(2)f(x)=2a·b+1=2(-cos2x+sinxcosx)+1
=2sinxcosx-(2cos2x-1)=sin2x-cos2x
=sin(2x-).
∵x∈[,],
∴2x-∈[,2π],
∴sin(2x-)∈[-1,],
∴当2x-=,即x=时,f(x)max=1.
20.(本小题满分12分)在△ABC中,角A、B、C所对的边长分别为a、b、c,已知向量m=(1,2sinA),n=(sinA,1+cosA),且满足m∥n,b+c=a.
(1)求角A的大小;
(2)求sin的值.
解:(1)∵m∥n,∴1+cosA=2sin2A,
即2cos2A+cosA-1=0,解得cosA=-1(舍去),cosA=.
又0<A<π,∴A=.
(2)∵b+c=a,
∴由正弦定理可得sinB+sinC=sinA=.
又C=π-(A+B)=-B,∴sinB+sin=,
即sinB+cosB=,∴sin=.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com