
9、 (2005重庆卷)
已知aÎR,讨论函数f(x)=ex(x2+ax+a+1)的极值点的个数。
8. (2005山东卷)
已知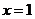 是函数
是函数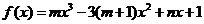 的一个极值点,其中
的一个极值点,其中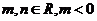 ,
,
(I)求 与
与 的关系式;
的关系式;
(II)求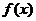 的单调区间;
的单调区间;
(III)当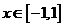 时,函数
时,函数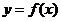 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 的取值范围.
的取值范围.
8、(2005辽宁卷)
函数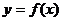 在区间(0,+∞)内可导,导函数
在区间(0,+∞)内可导,导函数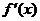 是减函数,且
是减函数,且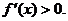 设
设 是曲线
是曲线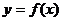 在点(
在点(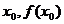 )得的切线方程,并设函数
)得的切线方程,并设函数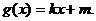
(Ⅰ)用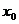 、
、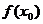 、
、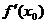 表示m;
表示m;
(Ⅱ)证明:当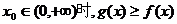 ;
;
(Ⅲ)若关于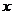 的不等式
的不等式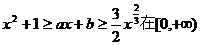 上恒成立,其中a、b为实数,
上恒成立,其中a、b为实数,
求b的取值范围及a与b所满足的关系.
7、(2005湖南卷)
已知函数f(x)=lnx,g(x)=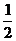 ax2+bx,a≠0.
ax2+bx,a≠0.
(Ⅰ)若b=2,且h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
(Ⅱ)设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q,过线段PQ的中点作x轴的垂线分别交C1,C2于点M、N,证明C1在点M处的切线与C2在点N处的切线不平行.
6、(2005湖南卷)
设 ,点P(
,点P( ,0)是函数
,0)是函数 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(Ⅰ)用 表示a,b,c;
表示a,b,c;
(Ⅱ)若函数 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求 的取值范围.
的取值范围.
5、(2005湖北卷)
已知向量 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
解法1:依定义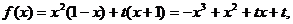
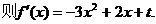
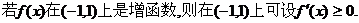
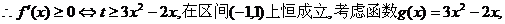
 开口向上的抛物线,故要使
开口向上的抛物线,故要使 在区间
在区间
(-1,1)上恒成立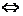
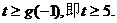
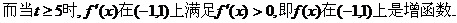
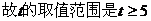 .
.
解法2:依定义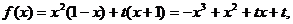
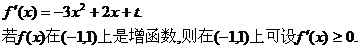
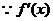 的图象是开口向下的抛物线,
的图象是开口向下的抛物线,

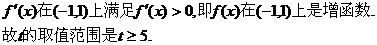
4、(2005福建卷)
已知函数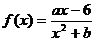 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
3、( 全国卷III)
已知函数 ,
,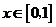
(Ⅰ)求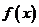 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设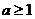 ,函数
,函数 ,若对于任意
,若对于任意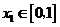 ,总存在
,总存在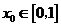 ,使得
,使得 成立,求
成立,求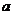 的取值范围
的取值范围
2、 (2005全国卷Ⅱ)
已知a≥ 0 ,函数f(x) = (  -2ax )
-2ax )
(1)当X为何值时,f(x)取得最小值?证明你的结论;
(2)设 f(x)在[ -1,1]上是单调函数,求a的取值范围.
1.(2005全国卷Ⅱ)
设a为实数,函数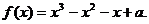
(Ⅰ)求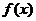 的极值.
的极值.
(Ⅱ)当a在什么范围内取值时,曲线 轴仅有一个交点.
轴仅有一个交点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com